Page 328 - Acquisition and Processing of Marine Seismic Data

6.2 ASSUMPTIONS FOR DECONVOLUTION 319

recorded seismogram can mathematically be these circumstances, Eq. (6.1) can only be solved
expressed as by considering a number of critical assumptions
∗ to accomplish the deconvolution process.
stðÞ ¼ wtðÞ rtðÞ + ntðÞ (6.1)
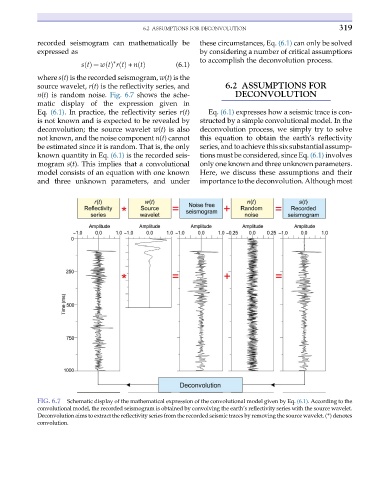
where s(t) is the recorded seismogram, w(t) is the
source wavelet, r(t) is the reflectivity series, and 6.2 ASSUMPTIONS FOR
n(t) is random noise. Fig. 6.7 shows the sche- DECONVOLUTION
matic display of the expression given in
Eq. (6.1). In practice, the reflectivity series r(t) Eq. (6.1) expresses how a seismic trace is con-
is not known and is expected to be revealed by structed by a simple convolutional model. In the
deconvolution; the source wavelet w(t) is also deconvolution process, we simply try to solve
not known, and the noise component n(t) cannot this equation to obtain the earth’s reflectivity
be estimated since it is random. That is, the only series,andto achieve this six substantial assump-
known quantity in Eq. (6.1) is the recorded seis- tions must be considered, since Eq. (6.1) involves
mogram s(t). This implies that a convolutional only one known and three unknown parameters.
model consists of an equation with one known Here, we discuss these assumptions and their
and three unknown parameters, and under importance to the deconvolution. Although most

FIG. 6.7 Schematic display of the mathematical expression of the convolutional model given by Eq. (6.1). According to the
convolutional model, the recorded seismogram is obtained by convolving the earth’s reflectivity series with the source wavelet.
Deconvolution aims to extract the reflectivity series from the recorded seismic traces by removing the source wavelet. (*)denotes
convolution.