Page 331 - Acquisition and Processing of Marine Seismic Data

322 6. DECONVOLUTION

source wavelet itself, is required to obtain the have a maximum value at zero lag, and they
deconvolution operator. Yet, how can we obtain exactly equal zero for all other lags. Such an
the autocorrelation of the source wavelet when autocorrelation function is actually a Dirac delta
we do not know the wavelet itself? The answer or unit impulse function (Table 4.1), and the con-
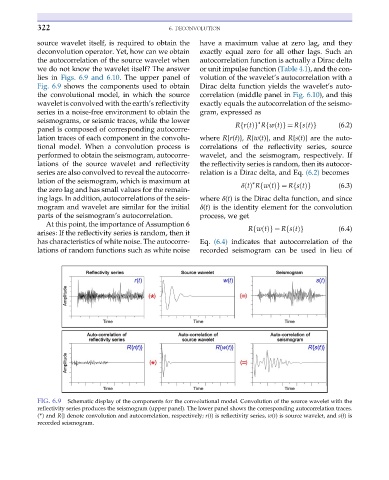
lies in Figs. 6.9 and 6.10. The upper panel of volution of the wavelet’s autocorrelation with a
Fig. 6.9 shows the components used to obtain Dirac delta function yields the wavelet’s auto-
the convolutional model, in which the source correlation (middle panel in Fig. 6.10), and this
wavelet is convolved with the earth’s reflectivity exactly equals the autocorrelation of the seismo-
series in a noise-free environment to obtain the gram, expressed as
seismograms, or seismic traces, while the lower ∗
f
Rr tðÞg Rw tðÞf g ¼ Rs tðÞg (6.2)
f
panel is composed of corresponding autocorre-
lation traces of each component in the convolu- where R{r(t)}, R{w(t)}, and R{s(t)} are the auto-
tional model. When a convolution process is correlations of the reflectivity series, source
performed to obtain the seismogram, autocorre- wavelet, and the seismogram, respectively. If
lations of the source wavelet and reflectivity the reflectivity series is random, then its autocor-
series are also convolved to reveal the autocorre- relation is a Dirac delta, and Eq. (6.2) becomes
lation of the seismogram, which is maximum at ∗
δ tðÞ Rw tðÞg ¼ Rs tðÞg (6.3)
f
f
the zero lag and has small values for the remain-
ing lags. In addition, autocorrelations of the seis- where δ(t) is the Dirac delta function, and since
mogram and wavelet are similar for the initial δ(t) is the identity element for the convolution
parts of the seismogram’s autocorrelation. process, we get
At this point, the importance of Assumption 6
Rw tðÞg ¼ Rs tðÞg (6.4)
f
f
arises: If the reflectivity series is random, then it
has characteristics of white noise. The autocorre- Eq. (6.4) indicates that autocorrelation of the
lations of random functions such as white noise recorded seismogram can be used in lieu of

FIG. 6.9 Schematic display of the components for the convolutional model. Convolution of the source wavelet with the
reflectivity series produces the seismogram (upper panel). The lower panel shows the corresponding autocorrelation traces.
(*) and R{} denote convolution and autocorrelation, respectively; r(t) is reflectivity series, w(t) is source wavelet, and s(t)is
recorded seismogram.