Page 77 - Adaptive Identification and Control of Uncertain Systems with Nonsmooth Dynamics

68 Adaptive Identification and Control of Uncertain Systems with Non-smooth Dynamics

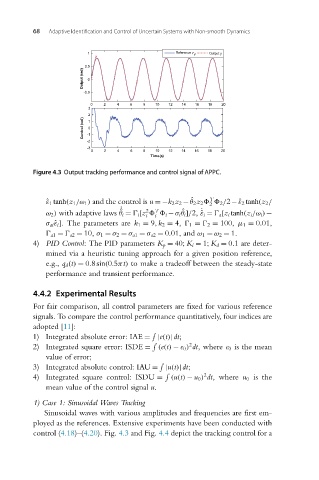
Figure 4.3 Output tracking performance and control signal of APPC.

T
ˆ
ˆ ε 1 tanh(z 1 /ω 1 ) and the control is u =−k 2z 2 −θ 2z 2 2 /2− ε 2 tanh(z 2 /
2
˙ 2 T ˙
ˆ
ˆ
ω 2 ) with adaptive laws θ i = i [z i −σ i θ i ]/2, ˆε i = a [z i tanh(z i /ω i )−
i
i
σ ai ˆε i ]. The parameters are k 1 = 9,k 2 = 4, 1 = 2 = 100, μ 1 = 0.01,
a1 = a2 = 10, σ 1 = σ 2 = σ a1 = σ a2 = 0.01, and ω 1 = ω 2 = 1.
4) PID Control: The PID parameters K p = 40;K i = 1;K d = 0.1 are deter-
mined via a heuristic tuning approach for a given position reference,
e.g., q d (t) = 0.8sin(0.5πt) to make a tradeoff between the steady-state
performance and transient performance.
4.4.2 Experimental Results
For fair comparison, all control parameters are fixed for various reference
signals. To compare the control performance quantitatively, four indices are
adopted [11]:

1) Integrated absolute error: IAE = |e(t)|dt;
2
2) Integrated square error: ISDE = (e(t) − e 0 ) dt,where e 0 is the mean
value of error;

3) Integrated absolute control: IAU = |u(t)|dt;
2
4) Integrated square control: ISDU = (u(t) − u 0 ) dt,where u 0 is the
mean value of the control signal u.
1) Case 1: Sinusoidal Waves Tracking
Sinusoidal waves with various amplitudes and frequencies are first em-
ployed as the references. Extensive experiments have been conducted with
control (4.18)–(4.20). Fig. 4.3 and Fig. 4.4 depict the tracking control for a