Page 827 - Advanced_Engineering_Mathematics o'neil

Answers to Selected Problems 807

6

4

2

0
0 2 4 6 8 10 12 14
t
–2

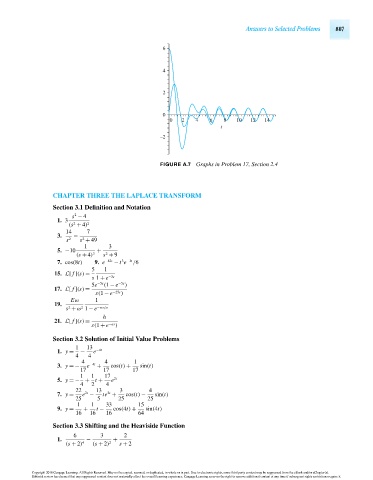
FIGURE A.7 Graphs in Problem 17, Section 2.4

CHAPTER THREE THE LAPLACE TRANSFORM
Section 3.1 Definition and Notation
2
s − 4
1. 3
2
(s + 4) 2
14 7
3. −
s 2 s + 49
2
1 3
5. −10 +
2
(s + 4) 3 s + 9
3 −3t
7. cos(8t) 9. e −42t − t e /6
5 1
15. L[ f ](s) =
s 1 + e −3s
5e −5s (1 − e −5s )
17. L[ f ](s) =
s(1 − e −25s )
Eω 1
19.
2
2
s + ω 1 − e −πs/ω
h
21. L[ f ](s) =
s(1 + e −as )
Section 3.2 Solution of Initial Value Problems
1 13
1. y = − e −4t
4 4
4 4 1
3. y =− e −4t + cos(t) + sin(t)
17 17 17
1 1 17
5. y =− + t + e 2t
4 2 4
22 13 3 4
2t
2t
7. y = e − te + cos(t) − sin(t)
25 5 25 25
1 1 33 15
9. y = + t − cos(4t) + sin(4t)
16 16 16 64
Section 3.3 Shifting and the Heaviside Function
6 3 2
1. − +
(s + 2) 4 (s + 2) 2 s + 2
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.
October 14, 2010 17:50 THM/NEIL Page-807 27410_25_Ans_p801-866