Page 359 - Advanced engineering mathematics

10.6 Phase Portraits 339

y

50
y(t)
(k/c, a/b)
40
II I
30
III IV
20

x(t) 10

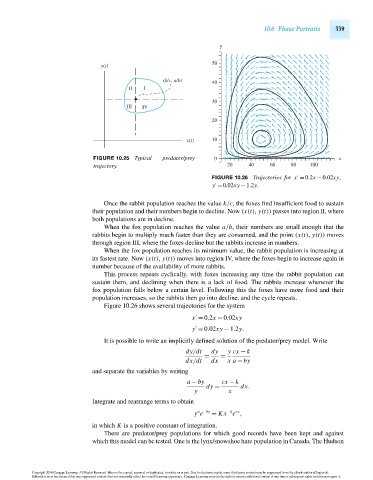
FIGURE 10.25 Typical predator/prey 0 x
trajectory. 20 40 60 80 100
FIGURE 10.26 Trajectories for x = 0.2x − 0.02xy,

y = 0.02xy − 1.2y.
Once the rabbit population reaches the value k/c, the foxes find insufficient food to sustain
their population and their numbers begin to decline. Now (x(t), y(t)) passes into region II, where
both populations are in decline.
When the fox population reaches the value a/b, their numbers are small enough that the
rabbits begin to multiply much faster than they are consumed, and the point (x(t), y(t)) moves
through region III, where the foxes decline but the rabbits increase in numbers.
When the fox population reaches its minimum value, the rabbit population is increasing at
its fastest rate. Now (x(t), y(t)) moves into region IV, where the foxes begin to increase again in
number because of the availability of more rabbits.
This process repeats cyclically, with foxes increasing any time the rabbit population can
sustain them, and declining when there is a lack of food. The rabbits increase whenever the
fox population falls below a certain level. Following this the foxes have more food and their
population increases, so the rabbits then go into decline, and the cycle repeats.
Figure 10.26 shows several trajectories for the system

x = 0.2x − 0.02xy

y = 0.02xy − 1.2y.
It is possible to write an implicitly defined solution of the predator/prey model. Write
dy/dt dy y cx − k
= =
dx/dt dx x a − by
and separate the variables by writing
a − by cx − k
dy = dx.
y x
Integrate and rearrange terms to obtain

−k cx
a −by
y e = Kx e ,
in which K is a positive constant of integration.
There are predator/prey populations for which good records have been kept and against
which this model can be tested. One is the lynx/snowshoe hare population in Canada. The Hudson

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 20:32 THM/NEIL Page-339 27410_10_ch10_p295-342