Page 154 - Advances in Biomechanics and Tissue Regeneration

150 8. TOWARDS THE REAL-TIME MODELING OF THE HEART

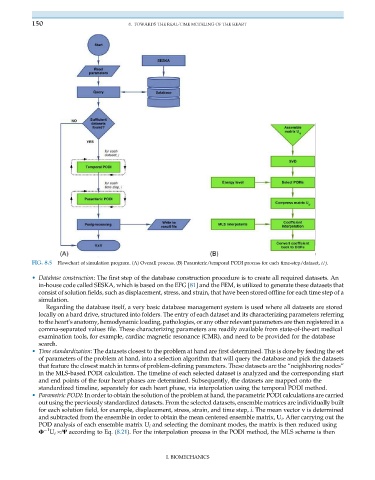
FIG. 8.5 Flowchart of simulation program. (A) Overall process. (B) Paramteric/temporal PODI process for each time-step/dataset, i/j.

• Database construction: The first step of the database construction procedure is to create all required datasets. An
in-house code called SESKA, which is based on the EFG [81] and the FEM, is utilized to generate these datasets that
consist of solution fields, such as displacement, stress, and strain, that have been stored offline for each time step of a
simulation.
Regarding the database itself, a very basic database management system is used where all datasets are stored
locally on a hard drive, structured into folders. The entry of each dataset and its characterizing parameters referring
to the heart’s anatomy, hemodynamic loading, pathologies, or any other relevant parameters are then registered in a
comma-separated values file. These characterizing parameters are readily available from state-of-the-art medical
examination tools, for example, cardiac magnetic resonance (CMR), and need to be provided for the database
search.
• Time standardization: The datasets closest to the problem at hand are first determined. This is done by feeding the set
of parameters of the problem at hand, into a selection algorithm that will query the database and pick the datasets
that feature the closest match in terms of problem-defining parameters. These datasets are the “neighboring nodes”
in the MLS-based PODI calculation. The timeline of each selected dataset is analyzed and the corresponding start
and end points of the four heart phases are determined. Subsequently, the datasets are mapped onto the
standardized timeline, separately for each heart phase, via interpolation using the temporal PODI method.
• Parametric PODI: In order to obtain the solution of the problem at hand, the parametric PODI calculations are carried
out using the previously standardized datasets. From the selected datasets, ensemble matrices are individually built
for each solution field, for example, displacement, stress, strain, and time step, i. The mean vector v is determined
and subtracted from the ensemble in order to obtain the mean centered ensemble matrix, U i . After carrying out the
POD analysis of each ensemble matrix U i and selecting the dominant modes, the matrix is then reduced using
1
Φ U i Ψ according to Eq. (8.21). For the interpolation process in the PODI method, the MLS scheme is then

I. BIOMECHANICS