Page 308 -

288 CHAPTER 7 TRANSPORTATION, ASSIGNMENT AND TRANSSHIPMENT PROBLEMS

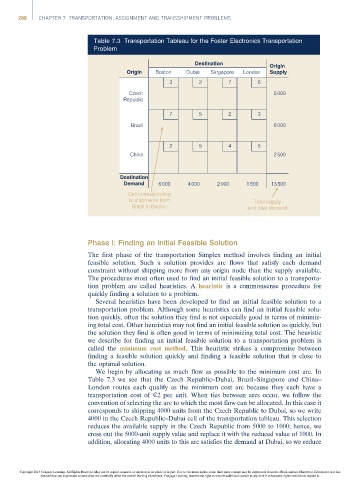
Table 7.3 Transportation Tableau for the Foster Electronics Transportation
Problem

Destination Origin
Origin Boston Dubai Singapore London Supply
3 2 7 6

Czech 5 000
Republic
7 5 2 3

Brazil 6 000

2 5 4 5
China 2 500

Destination
Demand 6 000 4 000 2 000 1 500 13 500
Cell corresponding
to shipments from Total supply
Brazil to Boston and total demand

Phase I: Finding an Initial Feasible Solution

The first phase of the transportation Simplex method involves finding an initial
feasible solution. Such a solution provides arc flows that satisfy each demand
constraint without shipping more from any origin node than the supply available.
The procedures most often used to find an initial feasible solution to a transporta-
tion problem are called heuristics. A heuristic is a commonsense procedure for
quickly finding a solution to a problem.
Several heuristics have been developed to find an initial feasible solution to a
transportation problem. Although some heuristics can find an initial feasible solu-
tion quickly, often the solution they find is not especially good in terms of minimiz-
ing total cost. Other heuristics may not find an initial feasible solution as quickly, but
the solution they find is often good in terms of minimizing total cost. The heuristic
we describe for finding an initial feasible solution to a transportation problem is
called the minimum cost method. This heuristic strikes a compromise between
finding a feasible solution quickly and finding a feasible solution that is close to
the optimal solution.
We begin by allocating as much flow as possible to the minimum cost arc. In
Table 7.3 we see that the Czech Republic–Dubai, Brazil–Singapore and China–
London routes each qualify as the minimum cost arc because they each have a
transportation cost of E2 per unit. When ties between arcs occur, we follow the
convention of selecting the arc to which the most flow can be allocated. In this case it
corresponds to shipping 4000 units from the Czech Republic to Dubai, so we write
4000 in the Czech Republic–Dubai cell of the transportation tableau. This selection
reduces the available supply in the Czech Republic from 5000 to 1000; hence, we
cross out the 5000-unit supply value and replace it with the reduced value of 1000. In
addition, allocating 4000 units to this arc satisfies the demand at Dubai, so we reduce

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.