Page 79 -

A MINIMIZATION PROBLEM 59

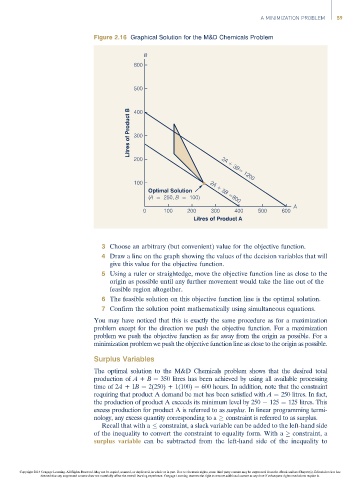
Figure 2.16 Graphical Solution for the M&D Chemicals Problem

B
600

500

Litres of Product B 400

300

200 2A + 3B= 1200

100
Optimal Solution 2A + 3B =800
(A = 250, B = 100)
A
0 100 200 300 400 500 600
Litres of Product A

3 Choose an arbitrary (but convenient) value for the objective function.
4 Draw a line on the graph showing the values of the decision variables that will
give this value for the objective function.
5 Using a ruler or straightedge, move the objective function line as close to the
origin as possible until any further movement would take the line out of the
feasible region altogether.
6 The feasible solution on this objective function line is the optimal solution.
7 Confirm the solution point mathematically using simultaneous equations.
You may have noticed that this is exactly the same procedure as for a maximization
problem except for the direction we push the objective function. For a maximization
problem we push the objective function as far away from the origin as possible. For a
minimization problem we push the objective function line as close to the origin as possible.

Surplus Variables
The optimal solution to the M&D Chemicals problem shows that the desired total
production of A + B ¼ 350 litres has been achieved by using all available processing
time of 2A +1B ¼ 2(250) + 1(100) ¼ 600 hours. In addition, note that the constraint
requiring that product A demand be met has been satisfied with A ¼ 250 litres. In fact,
the production of product A exceeds its minimum level by 250 125 ¼ 125 litres. This
excess production for product A is referred to as surplus. In linear programming termi-
nology, any excess quantity corresponding to a constraint is referred to as surplus.
Recall that with a constraint, a slack variable can be added to the left-hand side
of the inequality to convert the constraint to equality form. With a constraint, a
surplus variable can be subtracted from the left-hand side of the inequality to

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.