Page 84 -

64 CHAPTER 2 AN INTRODUCTION TO LINEAR PROGRAMMING

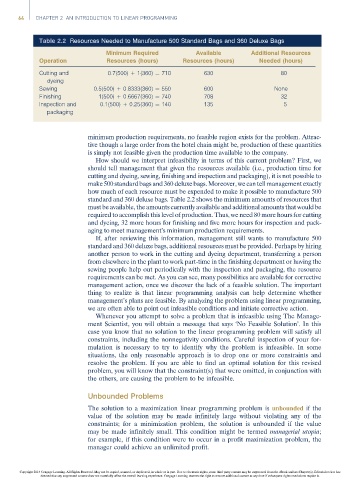
Table 2.2 Resources Needed to Manufacture 500 Standard Bags and 360 Deluxe Bags
Minimum Required Available Additional Resources
Operation Resources (hours) Resources (hours) Needed (hours)

Cutting and 0.7(500) + 1(360) ¼ 710 630 80
dyeing
Sewing 0.5(500) + 0.8333(360) ¼ 550 600 None
Finishing 1(500) + 0.6667(360) ¼ 740 708 32
Inspection and 0.1(500) + 0.25(360) ¼ 140 135 5
packaging

minimum production requirements, no feasible region exists for the problem. Attrac-
tive though a large order from the hotel chain might be, production of these quantities
is simply not feasible given the production time available to the company.
How should we interpret infeasibility in terms of this current problem? First, we
should tell management that given the resources available (i.e., production time for
cutting and dyeing, sewing, finishing and inspection and packaging), it is not possible to
make 500 standard bags and 360 deluxe bags. Moreover, we can tell management exactly
how much of each resource must be expended to make it possible to manufacture 500
standard and 360 deluxe bags. Table 2.2 shows the minimum amounts of resources that
must be available, the amounts currently available and additional amounts that would be
required to accomplish this level of production. Thus, we need 80 more hours for cutting
and dyeing, 32 more hours for finishing and five more hours for inspection and pack-
aging to meet management’s minimum production requirements.
If, after reviewing this information, management still wants to manufacture 500
standard and 360 deluxe bags, additional resources must be provided. Perhaps by hiring
another person to work in the cutting and dyeing department, transferring a person
from elsewhere in the plant to work part-time in the finishing department or having the
sewing people help out periodically with the inspection and packaging, the resource
requirements can be met. As you can see, many possibilities are available for corrective
management action, once we discover the lack of a feasible solution. The important
thing to realize is that linear programming analysis can help determine whether
management’s plans are feasible. By analyzing the problem using linear programming,
we are often able to point out infeasible conditions and initiate corrective action.
Whenever you attempt to solve a problem that is infeasible using The Manage-
ment Scientist, you will obtain a message that says ‘No Feasible Solution’. In this
case you know that no solution to the linear programming problem will satisfy all
constraints, including the nonnegativity conditions. Careful inspection of your for-
mulation is necessary to try to identify why the problem is infeasible. In some
situations, the only reasonable approach is to drop one or more constraints and
resolve the problem. If you are able to find an optimal solution for this revised
problem, you will know that the constraint(s) that were omitted, in conjunction with
the others, are causing the problem to be infeasible.

Unbounded Problems
The solution to a maximization linear programming problem is unbounded if the
value of the solution may be made infinitely large without violating any of the
constraints; for a minimization problem, the solution is unbounded if the value
may be made infinitely small. This condition might be termed managerial utopia;
for example, if this condition were to occur in a profit maximization problem, the
manager could achieve an unlimited profit.

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.