Page 85 -

SPECIAL CASES 65

However, in linear programming models of real problems, the occurrence of an
unbounded solution probably means that the problem has been improperly for-
mulated. We know it is not possible to increase profits indefinitely. Therefore, we
must conclude that if a profit maximization problem results in an unbounded
solution, the mathematical model doesn’t represent the real-world problem suffi-
ciently. Usually, what has happened is that a constraint has been omitted during
problem formulation.
As an illustration, consider the following linear programme with two decision
variables, X and Y:
Max 20X þ 10Y
s:t:
1X 2
1Y 5
X; Y 0
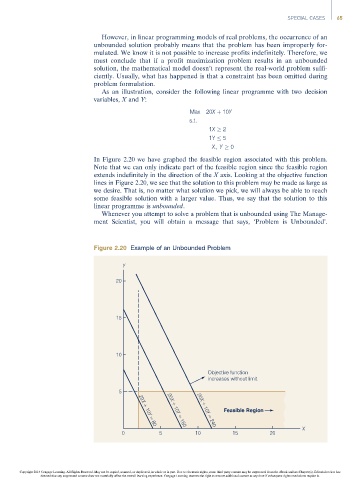
In Figure 2.20 we have graphed the feasible region associated with this problem.
Note that we can only indicate part of the feasible region since the feasible region
extends indefinitely in the direction of the X axis. Looking at the objective function
lines in Figure 2.20, we see that the solution to this problem may be made as large as
we desire. That is, no matter what solution we pick, we will always be able to reach
some feasible solution with a larger value. Thus, we say that the solution to this
linear programme is unbounded.
Whenever you attempt to solve a problem that is unbounded using The Manage-
ment Scientist, you will obtain a message that says, ‘Problem is Unbounded’.

Figure 2.20 Example of an Unbounded Problem

Y

20

15

10

Objective function
increases without limit.

5

Feasible Region

20 X + 10Y = 80
20 X + 10Y = 160
X
20 X + 10Y = 240
0 5 10 15 20

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.