Page 83 -

SPECIAL CASES 63

which is halfway between the two extreme points, also provides the optimal objective
function value of:
6:3S þ 9D ¼ 6:3ð420Þþ 9ð336Þ¼ 5670

A linear programming problem with alternative optimal solutions is generally a
good situation for the manager or decision maker. It means that several combina-
tions of the decision variables are optimal and that the manager can select the most
desirable optimal solution. Unfortunately, determining whether a problem has
alternative optimal solutions is not a simple matter.

Infeasibility
Problems with no Infeasibility means that no solution to the linear programming problem satisfies all
feasible solution do arise the constraints, including the nonnegativity conditions. Graphically, infeasibility
in practice, most often
because management’s means that a feasible region does not exist; that is, no points satisfy all the con-
expectations are too high straints and the nonnegativity conditions simultaneously. To illustrate this situation,
or because too many let us look again at the problem faced by GulfGolf.
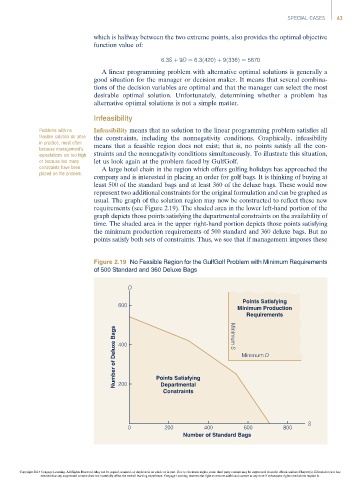
constraints have been A large hotel chain in the region which offers golfing holidays has approached the
placed on the problem.
company and is interested in placing an order for golf bags. It is thinking of buying at
least 500 of the standard bags and at least 360 of the deluxe bags. These would now
represent two additional constraints for the original formulation and can be graphed as
usual. The graph of the solution region may now be constructed to reflect these new
requirements (see Figure 2.19). The shaded area in the lower left-hand portion of the
graph depicts those points satisfying the departmental constraints on the availability of
time. The shaded area in the upper right-hand portion depicts those points satisfying
the minimum production requirements of 500 standard and 360 deluxe bags. But no
points satisfy both sets of constraints. Thus, we see that if management imposes these

Figure 2.19 No Feasible Region for the GulfGolf Problem with Minimum Requirements
of 500 Standard and 360 Deluxe Bags

D
Points Satisfying
600 Minimum Production
Requirements

Number of Deluxe Bags 400 Minimum S Minimum D

Points Satisfying
200
Departmental
Constraints

S
0 200 400 600 800
Number of Standard Bags

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.