Page 82 -

62 CHAPTER 2 AN INTRODUCTION TO LINEAR PROGRAMMING

2.6 Special Cases

In this section we discuss three special situations that can arise when we attempt to
solve linear programming problems.

Alternative Optimal Solutions
From the discussion of the graphical solution procedure, we know that optimal
solutions are found at the extreme points of the feasible region. Now let us consider
the special case in which the optimal objective function line coincides with one of the
binding constraint lines on the boundary of the feasible region. We will see that this
situation can lead to the case of alternative optimal solutions; in such cases, more
than one solution provides the optimal value for the objective function.
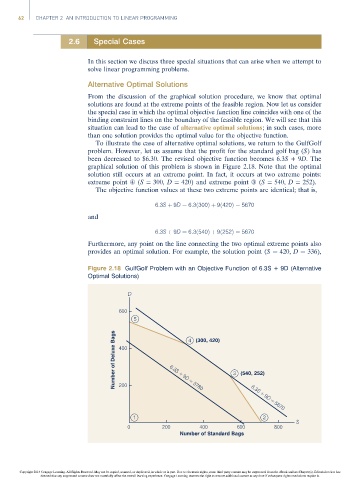
To illustrate the case of alternative optimal solutions, we return to the GulfGolf
problem. However, let us assume that the profit for the standard golf bag (S) has
been decreased to $6.30. The revised objective function becomes 6.3S +9D. The
graphical solution of this problem is shown in Figure 2.18. Note that the optimal
solution still occurs at an extreme point. In fact, it occurs at two extreme points:
extreme point fl (S ¼ 300, D ¼ 420) and extreme point fi (S ¼ 540, D ¼ 252).
The objective function values at these two extreme points are identical; that is,

6:3S þ 9D ¼ 6:3ð300Þþ 9ð420Þ¼ 5670
and

6:3S þ 9D ¼ 6:3ð540Þþ 9ð252Þ¼ 5670

Furthermore, any point on the line connecting the two optimal extreme points also
provides an optimal solution. For example, the solution point (S ¼ 420, D ¼ 336),

Figure 2.18 GulfGolf Problem with an Objective Function of 6.3S + 9D (Alternative
Optimal Solutions)

D

600
5

Number of Deluxe Bags 400 6.3S + 9D = 3780 3 (540, 252)
(300, 420)
4

200

6.3S + 9D = 5670
1 2
S
0 200 400 600 800
Number of Standard Bags

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.