Page 203 - Analysis and Design of Machine Elements

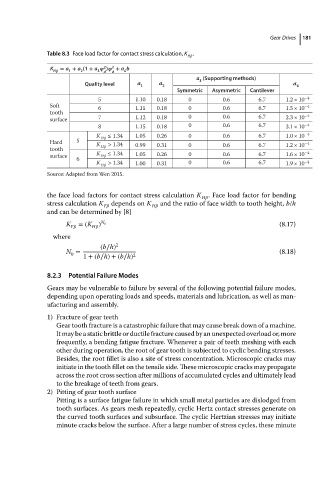
Table 8.3 Face load factor for contact stress calculation, K . Gear Drives 181
H
K = a + a (1 + a 2 ) 2 + a b
H 1 2 3 d d 4
a (Supporting methods)
3
Quality level a 1 a 2 a 4
Symmetric Asymmetric Cantilever
5 1.10 0.18 0 0.6 6.7 1.2 × 10 −4
Soft 6 1.11 0.18 0 0.6 6.7 1.5 × 10 −4
tooth −4
surface 7 1.12 0.18 0 0.6 6.7 2.3 × 10
8 1.15 0.18 0 0.6 6.7 3.1 × 10 −4
K H ≤ 1.34 1.05 0.26 0 0.6 6.7 1.0 × 10 −4
Hard 5 K > 1.34 0.99 0.31 0 0.6 6.7 1.2 × 10 −4
tooth H −4
surface K H ≤ 1.34 1.05 0.26 0 0.6 6.7 1.6 × 10
6
K H > 1.34 1.00 0.31 0 0.6 6.7 1.9 × 10 −4
Source: Adapted from Wen 2015.

the face load factors for contact stress calculation K H . Face load factor for bending
stress calculation K F depends on K H and the ratio of face width to tooth height, b/h
and can be determined by [8]
K F =(K ) N 0 (8.17)
H
where
(b∕h) 2
N = (8.18)
0
1 +(b∕h)+(b∕h) 2

8.2.3 Potential Failure Modes
Gears may be vulnerable to failure by several of the following potential failure modes,
depending upon operating loads and speeds, materials and lubrication, as well as man-
ufacturing and assembly.
1) Fracture of gear teeth
Gear tooth fracture is a catastrophic failure that may cause break down of a machine.
It may be a static brittle or ductile fracture caused by an unexpected overload or, more
frequently, a bending fatigue fracture. Whenever a pair of teeth meshing with each
other during operation, the root of gear tooth is subjected to cyclic bending stresses.
Besides, the root fillet is also a site of stress concentration. Microscopic cracks may
initiate in the tooth fillet on the tensile side. These microscopic cracks may propagate
across the root cross section after millions of accumulated cycles and ultimately lead
to the breakage of teeth from gears.
2) Pitting of gear tooth surface
Pitting is a surface fatigue failure in which small metal particles are dislodged from
tooth surfaces. As gears mesh repeatedly, cyclic Hertz contact stresses generate on
the curved tooth surfaces and subsurface. The cyclic Hertzian stresses may initiate
minute cracks below the surface. After a large number of stress cycles, these minute