Page 254 - Applied Numerical Methods Using MATLAB

DOUBLE INTEGRAL 243

1

2
0.5 z = 1 − x − y 2

y = 1 − x 2

0 (x, y)
1
y 1
x
0.5
0
0 −1

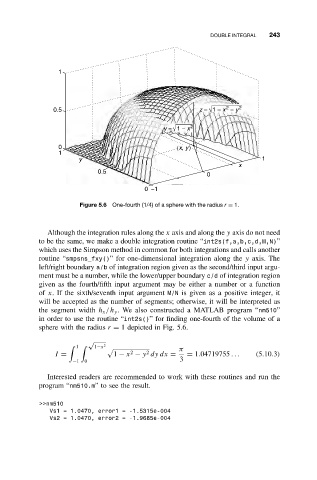
Figure 5.6 One-fourth (1/4) of a sphere with the radius r = 1.

Although the integration rules along the x axis and along the y axis do not need
to be the same, we make a double integration routine “int2s(f,a,b,c,d,M,N)”
which uses the Simpson method in common for both integrations and calls another
routine “smpsns_fxy()” for one-dimensional integration along the y axis. The
left/right boundary a/b of integration region given as the second/third input argu-
ment must be a number, while the lower/upper boundary c/d of integration region
given as the fourth/fifth input argument may be either a number or a function
of x. If the sixth/seventh input argument M/N is given as a positive integer, it
will be accepted as the number of segments; otherwise, it will be interpreted as
the segment width h x /h y . We also constructed a MATLAB program “nm510”
in order to use the routine “int2s()” for finding one-fourth of the volume of a
sphere with the radius r = 1 depicted in Fig. 5.6.

√
2
1 1−x π
2 2
I = 1 − x − y dy dx = = 1.04719755 ... (5.10.3)
−1 0 3
Interested readers are recommended to work with these routines and run the
program “nm510.m” to see the result.

>>nm510
Vs1 = 1.0470, error1 = -1.5315e-004
Vs2 = 1.0470, error2 = -1.9685e-004