Page 256 - Applied Numerical Methods Using MATLAB

PROBLEMS 245

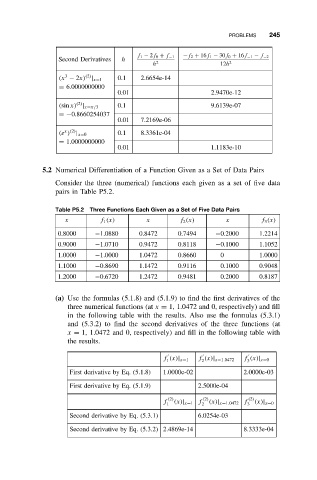
f 1 − 2f 0 + f −1 −f 2 + 16f 1 − 30f 0 + 16f −1 − f −2
Second Derivatives h
h 2 12h 2
3 (2)
(x − 2x) | x=1 0.1 2.6654e-14
= 6.0000000000
0.01 2.9470e-12
(2)
(sin x) | x=π/3 0.1 9.6139e-07
=−0.8660254037
0.01 7.2169e-06
x (2)
(e ) | x=0 0.1 8.3361e-04
= 1.0000000000
0.01 1.1183e-10

5.2 Numerical Differentiation of a Function Given as a Set of Data Pairs
Consider the three (numerical) functions each given as a set of five data
pairs in Table P5.2.

Table P5.2 Three Functions Each Given as a Set of Five Data Pairs
x f 1 (x) x f 2 (x) x f 3 (x)
0.8000 −1.0880 0.8472 0.7494 −0.2000 1.2214
0.9000 −1.0710 0.9472 0.8118 −0.1000 1.1052
1.0000 −1.0000 1.0472 0.8660 0 1.0000
1.1000 −0.8690 1.1472 0.9116 0.1000 0.9048
1.2000 −0.6720 1.2472 0.9481 0.2000 0.8187

(a) Use the formulas (5.1.8) and (5.1.9) to find the first derivatives of the
three numerical functions (at x = 1, 1.0472 and 0, respectively) and fill
in the following table with the results. Also use the formulas (5.3.1)
and (5.3.2) to find the second derivatives of the three functions (at
x = 1, 1.0472 and 0, respectively) and fill in the following table with
the results.

f (x)| x=1 f (x)| x=1.0472 f (x)| x=0
1
3
2
First derivative by Eq. (5.1.8) 1.0000e-02 2.0000e-03
First derivative by Eq. (5.1.9) 2.5000e-04
(2) (2) (2)
f (x)| x=1 f (x)| x=1.0472 f
1 2 3 (x)| x=0
Second derivative by Eq. (5.3.1) 6.0254e-03
Second derivative by Eq. (5.3.2) 2.4869e-14 8.3333e-04