Page 313 - Applied Numerical Methods Using MATLAB

302 ORDINARY DIFFERENTIAL EQUATIONS

function spring(n,p1,p2,w,color)
%draw a spring of n windings, width w from p1 to p2
if nargin < 5, color = ’k’; end
c = (p2(1) - p1(1))/2; d = (p2(2) - p1(2))/2;
f = (p2(1) + p1(1))/2; g = (p2(2) + p1(2))/2;
y = -1:0.01:1; t = (y+1)*pi*(n + 0.5);
x = -0.5*w*sin(t); y = y+0.15*(1 - cos(t));
a = y(1); b=y(length(x));
y = 2*(y - a)/(b - a)-1;
yyS = d*y - c*x + g; xxS = x+f; xxS1 = [f f];
yyS1 = yyS(length(yyS))+[0 w]; yyS2 = yyS(1)-[0 w];
plot(xxS,yyS,color, xxS1,yyS1,color, xxS1,yyS2,color)
function damper(xm,y1,y2,w,color)
%draws a damper in (xm-0.5 xm + 0.5 y1 y2)
if nargin < 5, color = ’k’; end
ym = (y1 + y2)/2;
xD1 = xm + w*[0.3*[0 0 -1 1]]; yD1 = [y2 + w ym ym ym];
xD2 = xm + w*[0.5*[-1 -1 1 1]]; yD2 = ym + w*[1 -1 -1
1];
xD3 = xm + [0 0]; yD3 = [y1 ym] - w;
plot(xD1,yD1,color, xD2,yD2,color, xD3,yD3,color)
function wheel_my(xm,ym,w,color)
%draws a wheel of size w at center (xm,ym)
if nargin < 5, color = ’k’; end
xW1 = xm + w*1.2*[-1 1]; yW1 = ym + w*[2 2];
xW2 = xm*[1 1]; yW2 = ym + w*[2 0];
plot(xW1,yW1,color, xW2,yW2,color)
th = [0:100]/50*pi; plot(xm + j*ym+w*exp(j*th),color)

1.2
M y(t) 1 u(t)

0.8
0.6
K B
0.4
u(t)
0.2
0 y(t)

−0.2
0 2 4 6 8 10
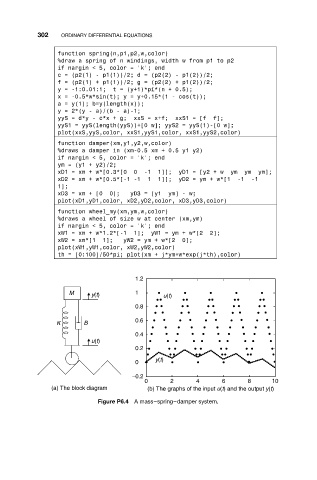
(a) The block diagram (b) The graphs of the input u(t) and the output y(t)
Figure P6.4 A mass–spring–damper system.