Page 82 - Applied Petroleum Geomechanics

Rock physical and mechanical properties 73

Poisson's ratio
0 0.1 0.2 0.3 0.4 0.5
2000

2500
)
m
(

r
o
o
l
f 3000

a
e
s

m
o
r
f

h
t 3500
p
e
D
4000
4500
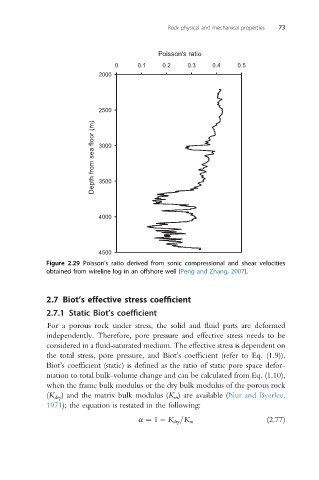
Figure 2.29 Poisson’s ratio derived from sonic compressional and shear velocities
obtained from wireline log in an offshore well (Peng and Zhang, 2007).

2.7 Biot’s effective stress coefficient
2.7.1 Static Biot’s coefficient
For a porous rock under stress, the solid and fluid parts are deformed
independently. Therefore, pore pressure and effective stress needs to be
considered in a fluid-saturated medium. The effective stress is dependent on
the total stress, pore pressure, and Biot’s coefficient (refer to Eq. (1.9)).
Biot’s coefficient (static) is defined as the ratio of static pore space defor-
mation to total bulk-volume change and can be calculated from Eq. (1.10),
when the frame bulk modulus or the dry bulk modulus of the porous rock
(K dry ) and the matrix bulk modulus (K m ) are available (Nur and Byerlee,
1971); the equation is restated in the following:

a ¼ 1 K dry =K m (2.77)