Page 237 - Applied Statistics And Probability For Engineers

c06.qxd 5/14/02 9:54 M Page 198 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

198 CHAPTER 6 RANDOM SAMPLING AND DATA DESCRIPTION

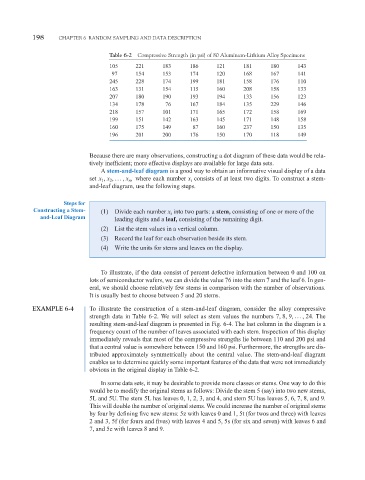
Table 6-2 Compressive Strength (in psi) of 80 Aluminum-Lithium Alloy Specimens
105 221 183 186 121 181 180 143
97 154 153 174 120 168 167 141
245 228 174 199 181 158 176 110
163 131 154 115 160 208 158 133
207 180 190 193 194 133 156 123
134 178 76 167 184 135 229 146
218 157 101 171 165 172 158 169
199 151 142 163 145 171 148 158
160 175 149 87 160 237 150 135
196 201 200 176 150 170 118 149

Because there are many observations, constructing a dot diagram of these data would be rela-
tively inefficient; more effective displays are available for large data sets.
A stem-and-leaf diagram is a good way to obtain an informative visual display of a data
set x , x , p , x , where each number x i consists of at least two digits. To construct a stem-
1
n
2
and-leaf diagram, use the following steps.
Steps for
Constructing a Stem- (1) Divide each number x into two parts: a stem, consisting of one or more of the
i
and-Leaf Diagram
leading digits and a leaf, consisting of the remaining digit.
(2) List the stem values in a vertical column.
(3) Record the leaf for each observation beside its stem.
(4) Write the units for stems and leaves on the display.

To illustrate, if the data consist of percent defective information between 0 and 100 on
lots of semiconductor wafers, we can divide the value 76 into the stem 7 and the leaf 6. In gen-
eral, we should choose relatively few stems in comparison with the number of observations.
It is usually best to choose between 5 and 20 stems.
EXAMPLE 6-4 To illustrate the construction of a stem-and-leaf diagram, consider the alloy compressive
strength data in Table 6-2. We will select as stem values the numbers 7, 8, 9, p , 24. The
resulting stem-and-leaf diagram is presented in Fig. 6-4. The last column in the diagram is a
frequency count of the number of leaves associated with each stem. Inspection of this display
immediately reveals that most of the compressive strengths lie between 110 and 200 psi and
that a central value is somewhere between 150 and 160 psi. Furthermore, the strengths are dis-
tributed approximately symmetrically about the central value. The stem-and-leaf diagram
enables us to determine quickly some important features of the data that were not immediately
obvious in the original display in Table 6-2.

In some data sets, it may be desirable to provide more classes or stems. One way to do this
would be to modify the original stems as follows: Divide the stem 5 (say) into two new stems,
5L and 5U. The stem 5L has leaves 0, 1, 2, 3, and 4, and stem 5U has leaves 5, 6, 7, 8, and 9.
This will double the number of original stems. We could increase the number of original stems
by four by defining five new stems: 5z with leaves 0 and 1, 5t (for twos and three) with leaves
2 and 3, 5f (for fours and fives) with leaves 4 and 5, 5s (for six and seven) with leaves 6 and
7, and 5e with leaves 8 and 9.