Page 143 - Applied statistics and probability for engineers

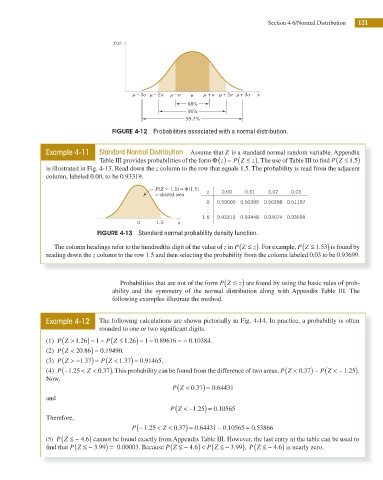
Section 4-6/Normal Distribution 121

f (x)

m – 3s m – 2s m – s m m + s m + 2s m + 3s x
68%
95%
99.7%
FIGURE 4-12 Probabilities associated with a normal distribution.

Example 4-11 Standard Normal Distribution Assume that Z is a standard normal random variable. Appendix
(
z
Table III provides probabilities of the form Φ( ) = (Z ≤ ). The use of Table III to i nd P Z ≤ . ) 5
P
z
1
is illustrated in Fig. 4-13. Read down the z column to the row that equals 1.5. The probability is read from the adjacent
column, labeled 0.00, to be 0.93319.
P(Z # 1.5) = F(1.5) z 0.00 0.01 0.02 0.03
= shaded area
0 0.50000 0.50399 0.50398 0.51197
. . . . . .
1.5 0.93319 0.93448 0.93574 0.93699
0 1.5 z
FIGURE 4-13 Standard normal probability density function.
(
(
The column headings refer to the hundredths digit of the value of z in P Z ≤ z). For example, P Z ≤ . ) is found by
1 53
reading down the z column to the row 1.5 and then selecting the probability from the column labeled 0.03 to be 0.93699.

(
Probabilities that are not of the form P Z # z) are found by using the basic rules of prob-
ability and the symmetry of the normal distribution along with Appendix Table III. The
following examples illustrate the method.

Example 4-12 The following calculations are shown pictorially in Fig. 4-14. In practice, a probability is often
rounded to one or two signii cant digits.
(1) P Z > 1 26) = − ( 1 26) = 1 0 89616 = = 0 10384.
(
.
.
.
.
−
P Z ≤
1
(
(2) P Z < 20 86) = 0 19490.
.
.
(
(3) P Z > − . ) = ( 1 37 0
P Z < . ) = .91465.
1 37
. ). This probability can be found from the difference of two areas, P Z < 0 37) − (
(
(4) P − .25 < Z < 0 37 ( . P Z < − 1 25).
.
1
Now,
(
P Z < 0 37. ) = .
0 64431
and
(
P Z < − . ) = .1 25 0 10565
Therefore,
(
P − . 1 25 < Z < 0 . ) = .37 0 64431 − .10565 = .53866
0
0
(
(5) P Z ≤ − . ) 6 cannot be found exactly from Appendix Table III. However, the last entry in the table can be used to
4
(
(
(
(
99
3
i nd that P Z ≤ − . ) = 0 .00003 Because P Z ≤ − . ) 6 < P Z ≤ − . ) , P Z ≤ − . ) 6 is nearly zero.
4
3 99
4
.