Page 158 - Artificial Intelligence for Computational Modeling of the Heart

130 Chapter 4 Data-driven reduction of cardiac models

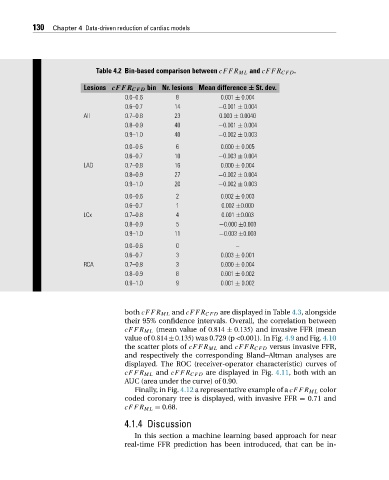
Table 4.2 Bin-based comparison between cFFR ML and cFFR CFD .

Lesions cFFR CFD bin Nr. lesions Mean difference ± St. dev.
0.0–0.6 8 0.001 ± 0.004
0.6–0.7 14 −0.001 ± 0.004
All 0.7–0.8 23 0.000 ± 0.0040
0.8–0.9 40 −0.001 ± 0.004
0.9–1.0 40 −0.002 ± 0.003
0.0–0.6 6 0.000 ± 0.005
0.6–0.7 10 −0.003 ± 0.004
LAD 0.7–0.8 16 0.000 ± 0.004
0.8–0.9 27 −0.002 ± 0.004
0.9–1.0 20 −0.002 ± 0.003
0.0–0.6 2 0.002 ± 0.003
0.6–0.7 1 0.002 ±0.000
LCx 0.7–0.8 4 0.001 ±0.003
0.8–0.9 5 −0.000 ±0.003
0.9–1.0 11 −0.003 ±0.003
0.0–0.6 0 –
0.6–0.7 3 0.003 ± 0.001
RCA 0.7–0.8 3 0.000 ± 0.004
0.8–0.9 8 0.001 ± 0.002
0.9–1.0 9 0.001 ± 0.002

both cFFR ML and cFFR CFD are displayed in Table 4.3, alongside
their 95% confidence intervals. Overall, the correlation between
cFFR ML (mean value of 0.814 ± 0.135) and invasive FFR (mean
value of 0.814±0.135) was 0.729 (p <0.001). In Fig. 4.9 and Fig. 4.10
the scatter plots of cFFR ML and cFFR CFD versus invasive FFR,
and respectively the corresponding Bland–Altman analyses are
displayed. The ROC (receiver-operator characteristic) curves of
cFFR ML and cFFR CFD are displayed in Fig. 4.11, both with an
AUC (area under the curve) of 0.90.
Finally, in Fig. 4.12 a representative example of a cFFR ML color
coded coronary tree is displayed, with invasive FFR = 0.71 and
cFFR ML = 0.68.

4.1.4 Discussion
In this section a machine learning based approach for near
real-time FFR prediction has been introduced, that can be in-