Page 25 - Artificial Intelligence in the Age of Neural Networks and Brain Computing

12 CHAPTER 1 Nature’s Learning Rule: The Hebbian-LMS Algorithm

(A)

(B)
k e

Negative stable Positive stable
equilibrium point equilibrium point
+ +
Sum
– –

Unstable
equilibrium point
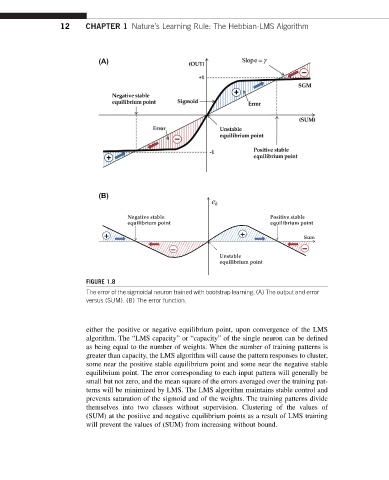
FIGURE 1.8
The error of the sigmoidal neuron trained with bootstrap learning. (A) The output and error
versus (SUM). (B) The error function.

either the positive or negative equilibrium point, upon convergence of the LMS
algorithm. The “LMS capacity” or “capacity” of the single neuron can be defined
as being equal to the number of weights. When the number of training patterns is
greater than capacity, the LMS algorithm will cause the pattern responses to cluster,
some near the positive stable equilibrium point and some near the negative stable
equilibrium point. The error corresponding to each input pattern will generally be
small but not zero, and the mean square of the errors averaged over the training pat-
terns will be minimized by LMS. The LMS algorithm maintains stable control and
prevents saturation of the sigmoid and of the weights. The training patterns divide
themselves into two classes without supervision. Clustering of the values of
(SUM) at the positive and negative equilibrium points as a result of LMS training
will prevent the values of (SUM) from increasing without bound.