Page 303 - Autonomous Mobile Robots

290 Autonomous Mobile Robots

60
40
20
n 1 (v) 0
– 20
– 40
– 60
0 5 10 15 20 25 30
Time (sec)
60
40
20
n 2 (v) 0

– 20
– 40
– 60
0 5 10 15 20 25 30
Time (sec)
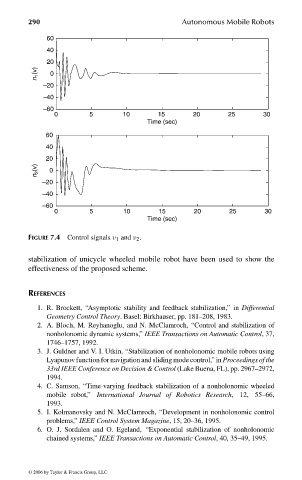
FIGURE 7.4 Control signals ν 1 and ν 2 .

stabilization of unicycle wheeled mobile robot have been used to show the
effectiveness of the proposed scheme.

REFERENCES

1. R. Brockett, “Asymptotic stability and feedback stabilization,” in Differential
Geometry Control Theory. Basel: Birkhauser, pp. 181–208, 1983.
2. A. Bloch, M. Reyhanoglu, and N. McClamroch, “Control and stabilization of
nonholonomic dynamic systems,” IEEE Transactions on Automatic Control, 37,
1746–1757, 1992.
3. J. Guldner and V. I. Utkin, “Stabilization of nonholonomic mobile robots using
Lyapunov function for navigation and sliding mode control,” in Proceedings of the
33rd IEEE Conference on Decision & Control (Lake Buena, FL), pp. 2967–2972,
1994.
4. C. Samson, “Time-varying feedback stabilization of a nonholonomic wheeled
mobile robot,” International Journal of Robotics Research, 12, 55–66,
1993.
5. I. Kolmanovsky and N. McClamroch, “Development in nonholonomic control
problems,” IEEE Control System Magazine, 15, 20–36, 1995.
6. O. J. Sordalen and O. Egeland, “Exponential stabilization of nonholonomic
chained systems,” IEEE Transactions on Automatic Control, 40, 35–49, 1995.

© 2006 by Taylor & Francis Group, LLC

FRANKL: “dk6033_c007” — 2006/3/31 — 16:43 — page 290 — #24