Page 120 - Bebop to The Boolean Boogie An Unconventional Guide to Electronics Fundamentals, Components, and Processes

Karnaugh Maps 101
c K
e< 00 01 11 10

00

01

11

10

11 c5 00 I 01 I 11 , 10 ,
y = (c &2) y = (a & b) I (c&d)

c 00 01 11 10 cx 00 01 10

y = (Z & d) y = (sj & b) I (b&Z) y = (b & d) I (a &e)

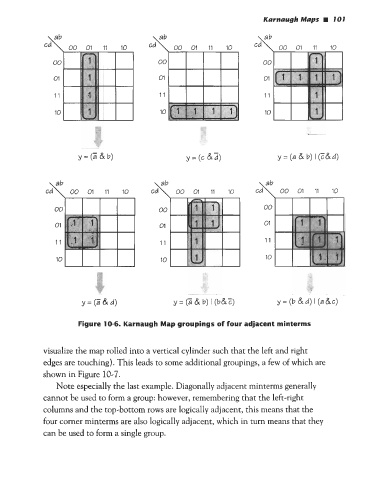
Figure 10-6. Karnaugh Map groupings of four adjacent minterms

visualize the map rolled into a vertical cylinder such that the left and right
edges are touching). This leads to some additional groupings, a few of which are
shown in Figure 10-7.
Note especially the last example. Diagonally adjacent minterms generally
cannot be used to form a group: however, remembering that the left-right
columns and the top-bottom rows are logically adjacent, this means that the
four corner minterms are also logically adjacent, which in turn means that they
can be used to form a single group.