Page 175 - Biaxial Multiaxial Fatigue and Fracture

I60 1 LIU AND H. ZENNER

STATISTICAL EVALUATION

As a check on the accuracy, the ratio x of the experimentally determined value to the calculated
value of the fatigue limit is employed for such an evaluation:

where o~,~? denotes the estimated average value of the experimentally determined
fatigue limit. For the calculation of axd.cal in accordance with SM, the estimated average
values of wand OS& are taken as a basis. At x = 1, the result of the calculation is equal to the
experimental result. At x>l, the fatigue limit with the SM is underestimated; at 61, the fatigue
limit is overestimated.
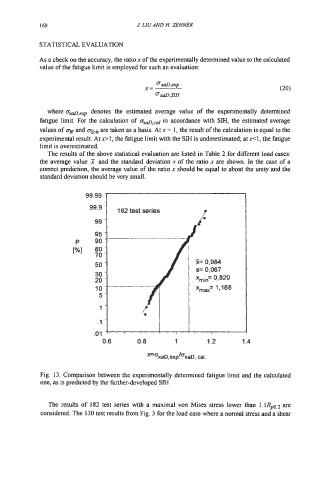
The results of the above statistical evaluation are listed in Table 2 for different load cases:
the average value .Y and the standard deviation s of the ratio x are shown. In the case of a
correct prediction, the average value of the ratio x should be equal to about the unity and the
standard deviation should be very small.

99.99
99.9
182 test series f
99
95
P
I%? ;E 90

50
30
20
10
5
1
.l
.01

Fig. 13. Comparison between the experimentally determined fatigue limit and the calculated
one, as is predicted by the further-developed SM

The results of 182 test series with a maximal von Mises stress lower than 1.1Rpo,2 are
considered. The 130 test results from Fig. 3 for the load case where a normal stress and a shear