Page 173 - Biaxial Multiaxial Fatigue and Fracture

158 1 LEU AND H. ZENNER

-
SIH
1.2 0 34Cr4 [28]
1.1 -1 0 St35 [ll]

0.6 ! I I I I I I I
1 2 3 4 5 6 7 8
frequency ratio $

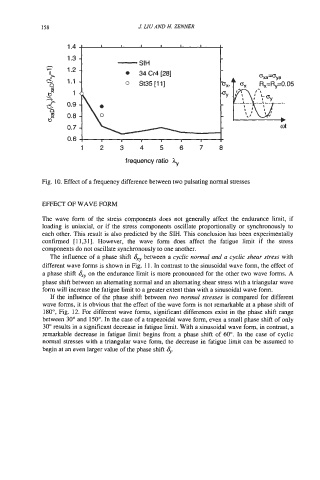
Fig. 10. Effect of a frequency difference between two pulsating normal stresses

EFFECT OF WAVE FORM
The wave form of the stress components does not generally affect the endurance limit, if
loading is uniaxial, or if the stress components oscillate proportionally or synchronously to
each other. This result is also predicted by the SM. This conclusion has been experimentally
confirmed [11,31]. However, the wave form does affect the fatigue limit if the stress
components do not oscillate synchronously to one another.
The influence of a phase shift 8, between a cyclic noma1 and a cyclic shear stress with
different wave forms is shown in Fig. 11. In contrast to the sinusoidal wave form, the effect of
a phase shift b&, on the endurance limit is more pronounced for the other two wave forms. A
phase shift between an alternating normal and an alternating shear stress with a triangular wave
form will increase the fatigue limit to a greater extent than with a sinusoidal wave form.
If the influence of the phase shift between two normal stresses is compared for different
wave forms, it is obvious that the effect of the wave form is not remarkable at a phase shift of
180", Fig. 12. For different wave forms, significant differences exist in the phase shift range
between 30" and 150". In the case of a trapezoidal wave form, even a small phase shift of only
30" results in a significant decrease in fatigue limit. With a sinusoidal wave form, in contrast, a
remarkable decrease in fatigue limit begins from a phase shift of 60". In the case of cyclic
normal stresses with a triangular wave form, the decrease in fatigue limit can be assumed to
begin at an even larger value of the phase shift 4.