Page 172 - Biaxial Multiaxial Fatigue and Fracture

Fatigue Limit of Ductile Metals Under Multiaxial Loading 157

corresponds to the case of torsional loading. The minimum of the fatigue limit is situated here.
The effect of the phase shift b; is correctly described by the SIH.

EFFECT OF FREQUENCY DIFFERENCE

In the case of uniaxial loading, the fatigue limit of metallic materials can usually be regarded as
frequency-independent. In the case of multiaxial loading, however, the frequency difference
between the stress components plays an important role. In contrast to the influence of the phase
shift, considerably less attention has been paid to the experimental behaviour of the fatigue
strength in the presence of differences in frequency of the stress components.
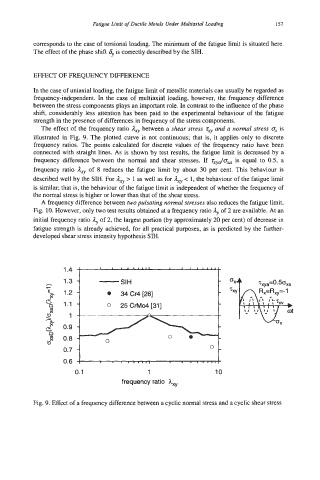
The effect of the frequency ratio Axy between a shear stress zXu and a nom1 stress ox is
illustrated in Fig. 9. The plotted curve is not continuous; that is, it applies only to discrete
frequency ratios. The points calculated for discrete values of the frequency ratio have been
connected with straight lines. As is shown by test results, the fatigue limit is decreased by a
frequency difference between the normal and shear stresses. If z,do,, is equal to 0.5, a
frequency ratio Ag of 8 reduces the fatigue limit by about 30 per cent. This behaviour is
described well by the SM. For Av > 1 as well as for & c 1, the behaviour of the fatigue limit
is similar; that is, the behaviour of the fatigue limit is independent of whether the frequency of
the normal stress is higher or lower than that of the shear stress.
A frequency difference between two pulsating normal stresses also reduces the fatigue limit,
Fig. 10. However, only two test results obtained at a frequency ratio 4 of 2 are available. At an
initial frequency ratio A,, of 2, the largest portion (by approximately 20 per cent) of decrease in
fatigue strength is already achieved, for all practical purposes, as is predicted by the further-
developed shear stress intensity hypothesis SIH.

- 1.4 j
- 1.3 - -
SIH
7
1% 1.2 - 34 Cr4 1281
55. 1.1 - 25CrMo4[31]
a 0
. 1-
D
3 0.9 -
n
0 0.8 - 0
fl
0.7 - 0

0.6 5 I
0.1 1 10
frequency ratio

Fig. 9. Effect of a frequency difference between a cyclic normal stress and a cyclic shear stress