Page 112 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

PHYSICAL AND FLOW PROPERTIES OF BLOOD 89

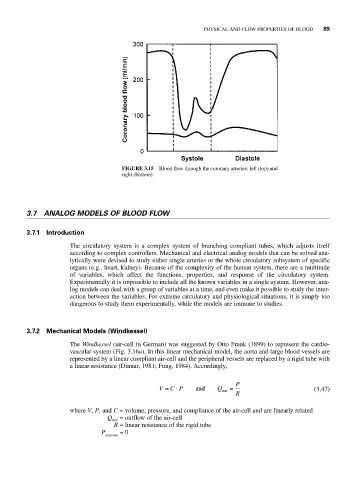
FIGURE 3.15 Blood flow through the coronary arteries: left (top) and
right (bottom).

3.7 ANALOG MODELS OF BLOOD FLOW

3.7.1 Introduction
The circulatory system is a complex system of branching compliant tubes, which adjusts itself
according to complex controllers. Mechanical and electrical analog models that can be solved ana-
lytically were devised to study either single arteries or the whole circulatory subsystem of specific
organs (e.g., heart, kidney). Because of the complexity of the human system, there are a multitude
of variables, which affect the functions, properties, and response of the circulatory system.
Experimentally it is impossible to include all the known variables in a single system. However, ana-
log models can deal with a group of variables at a time, and even make it possible to study the inter-
action between the variables. For extreme circulatory and physiological situations, it is simply too
dangerous to study them experimentally, while the models are immune to studies.

3.7.2 Mechanical Models (Windkessel)
The Windkessel (air-cell in German) was suggested by Otto Frank (1899) to represent the cardio-
vascular system (Fig. 3.16a). In this linear mechanical model, the aorta and large blood vessels are
represented by a linear compliant air-cell and the peripheral vessels are replaced by a rigid tube with
a linear resistance (Dinnar, 1981; Fung, 1984). Accordingly,

P
V = C P and Q out = (3.47)
•
R
where V, P, and C = volume, pressure, and compliance of the air-cell and are linearly related
Q out = outflow of the air-cell
R = linear resistance of the rigid tube
P = 0
venous