Page 238 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

BIODYNAMICS: A LAGRANGIAN APPROACH 215

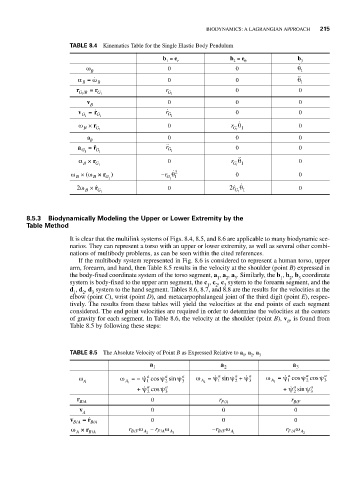
TABLE 8.4 Kinematics Table for the Single Elastic Body Pendulum
b = e b = e b
1 r 2 θ 3
ω 0 0 θ
B 1
α = B 0 0 θ 1
ω
B
r GB = r r 0 0
/
1 G 1 G 1
v 0 0 0
B
v = r r 0 0
G 1 G 1 G 1
ω × r G 1 0 r θ 0
Β
G 1 1
a 0 0 0
B
a = r r 0 0
G 1 G 1 G 1

α × r G 1 0 r θ 0
B
G 1 1
2
ω × ( ω × r G 1 ) −r θ 0 0
Β
Β
G 1 1
2ω × r G 0 2 r θ 0
Β
G
1 1
1
8.5.3 Biodynamically Modeling the Upper or Lower Extremity by the
Table Method
It is clear that the multilink systems of Figs. 8.4, 8.5, and 8.6 are applicable to many biodynamic sce-
narios. They can represent a torso with an upper or lower extremity, as well as several other combi-
nations of multibody problems, as can be seen within the cited references.
If the multibody system represented in Fig. 8.6 is considered to represent a human torso, upper
arm, forearm, and hand, then Table 8.5 results in the velocity at the shoulder (point B) expressed in
the body-fixed coordinate system of the torso segment, a , a , a . Similarly, the b , b , b coordinate
1 2 3 1 2 3
system is body-fixed to the upper arm segment, the c , c , c system to the forearm segment, and the
1 2 3
d , d , d system to the hand segment. Tables 8.6, 8.7, and 8.8 are the results for the velocities at the
1 2 3
elbow (point C), wrist (point D), and metacarpophalangeal joint of the third digit (point E), respec-
tively. The results from these tables will yield the velocities at the end points of each segment
considered. The end point velocities are required in order to determine the velocities at the centers
of gravity for each segment. In Table 8.6, the velocity at the shoulder (point B), v , is found from
B
Table 8.5 by following these steps:
TABLE 8.5 The Absolute Velocity of Point B as Expressed Relative to a , a , a
1 2 3
a 1 a 2 a 3
a
a
a
a
a
a
ω ω =− ψ cos ψ sin ψ a ω = ψ sin ψ + ψ a ω = ψ cos ψ cos ψ a 3
2
1
A A 1 1 2 3 A 2 1 2 3 A 3
a a a a
+ ψ cos ψ 3 + ψ sin ψ 3
2
2
r BA 0 r FA r BF
/
/
/
v 0 0 0
A
v = r 0 0 0
/
BA B A
/
ω × r B A r BF ω A 2 − r F A ω A 3 −r BF ω A 1 r FA ω A 2
/
/
/
/
/
A