Page 236 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

BIODYNAMICS: A LAGRANGIAN APPROACH 213

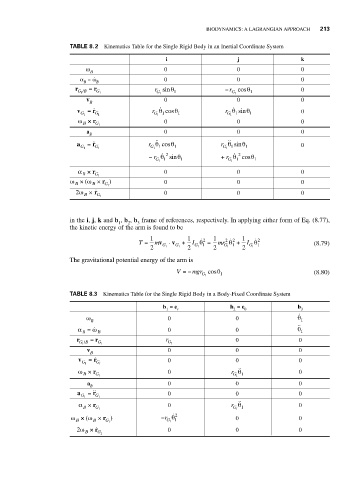
TABLE 8.2 Kinematics Table for the Single Rigid Body in an Inertial Coordinate System
i j k
ω 0 0 0
B
α =ω . 0 0 0
B B
r GB = r r sinθ −r cosθ 0
/
1 G 1 G 1 1 G 1 1
v 0 0 0
B

v = r r θ cos θ r θ sin θ 0
G 1 G 1 G 1 1 1 G 1 1 1
ω × r G 1 0 0 0
Β
a 0 0 0
B

a = r r θ cos θ r θ sin θ 0
G 1 G 1 G 1 1 1 G 1 1 1

2
2
− r θ sin θ + r θ cos θ
G 1 1 1 G 1 1 1
α × r G 1 0 0 0
B
ω × ( ω × r G 1 ) 0 0 0
Β
Β
2ω × r G 1 0 0 0
Β
in the i, j, k and b , b , b frame of references, respectively. In applying either form of Eq. (8.77),
3
2
1
the kinetic energy of the arm is found to be
1 1 2 1 2 2 1 2
T = mv • v + I θ = mr θ + I θ 2 (8.79)
G 1 1
G 1 1
G 1 1
2 G 1 G 1 2 2 2
The gravitational potential energy of the arm is
V =− mgr cosθ (8.80)
G 1 1
TABLE 8.3 Kinematics Table for the Single Rigid Body in a Body-Fixed Coordinate System
b = e b = e b
1 r 2 θ 3
ω 0 0 θ
B 1
α = Β 0 0 θ 1
ω
B
r GB = r r 0 0
/
1 G 1 G 1
v 0 0 0
B
v = r 0 0 0
G 1 G 1

ω × r G 1 0 r θ 0
Β
G 1 1
a 0 0 0
B
a = r 0 0 0
G 1 G 1

α × r G 1 0 r θ 0
B
G 1 1
2
ω × ( ω × r G 1 ) −r θ 0 0
Β
G 1 1
Β
2ω × r G 0 0 0
Β
1