Page 294 - Biomedical Engineering and Design Handbook Volume 1, Fundamentals

VIBRATION, MECHANICAL SHOCK, AND IMPACT 271

5
C / C = 0
c
x 1 (t)
m
0.125
4
k c
Transmissibility 3 0.25
x 0 (t)

2
0.5
1
1
C / C = 2
c
0
0 1 2 2 3 4 5
r = ω/ω o
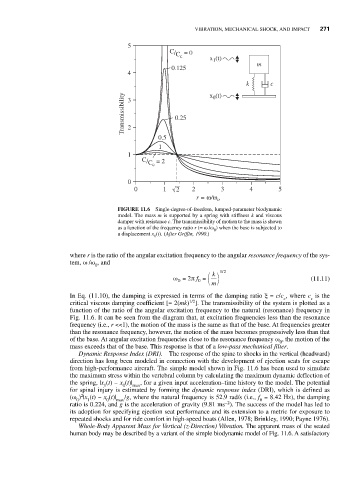
FIGURE 11.6 Single-degree-of-freedom, lumped-parameter biodynamic
model. The mass m is supported by a spring with stiffness k and viscous
damper with resistance c. The transmissibility of motion to the mass is shown
as a function of the frequency ratio r (= ω /ω ) when the base is subjected to
0
a displacement x (t). (After Griffin, 1990.)
0
where r is the ratio of the angular excitation frequency to the angular resonance frequency of the sys-
tem, ω /ω , and
0
12 /
⎛ k ⎞
ω = 2 π f = (11.11)
0
0
⎝ m ⎠
In Eq. (11.10), the damping is expressed in terms of the damping ratio ξ= c/c , where c is the
c
c
1/2
critical viscous damping coefficient [= 2(mk) ]. The transmissibility of the system is plotted as a
function of the ratio of the angular excitation frequency to the natural (resonance) frequency in
Fig. 11.6. It can be seen from the diagram that, at excitation frequencies less than the resonance
frequency (i.e., r <<1), the motion of the mass is the same as that of the base. At frequencies greater
than the resonance frequency, however, the motion of the mass becomes progressively less than that
of the base. At angular excitation frequencies close to the resonance frequency ω , the motion of the
0
mass exceeds that of the base. This response is that of a low-pass mechanical filter.
Dynamic Response Index (DRI). The response of the spine to shocks in the vertical (headward)
direction has long been modeled in connection with the development of ejection seats for escape
from high-performance aircraft. The simple model shown in Fig. 11.6 has been used to simulate
the maximum stress within the vertebral column by calculating the maximum dynamic deflection of
the spring, |x (t) − x (t)| , for a given input acceleration–time history to the model. The potential
1 0 max
for spinal injury is estimated by forming the dynamic response index (DRI), which is defined as
2
(ω ) |x (t) − x (t)| /g, where the natural frequency is 52.9 rad/s (i.e., f = 8.42 Hz), the damping
0 1 0 max 0
−2
ratio is 0.224, and g is the acceleration of gravity (9.81 ms ). The success of the model has led to
its adoption for specifying ejection seat performance and its extension to a metric for exposure to
repeated shocks and for ride comfort in high-speed boats (Allen, 1978; Brinkley, 1990; Payne 1976).
Whole-Body Apparent Mass for Vertical (z-Direction) Vibration. The apparent mass of the seated
human body may be described by a variant of the simple biodynamic model of Fig. 11.6. A satisfactory