Page 323 - Biomedical Engineering and Design Handbook Volume 2, Applications

THE PRINCIPLES OF X-RAY COMPUTED TOMOGRAPHY 301

modulation of intensity profiles is measured at steps along the grid taper, to provide the variation of
the contrast with frequency s. A spatial calibration and modulation reference is provided by an elec-
tron micrograph of the resolution standard. The measurements indicate that the resolving power of
the x-ray source has a bandwidth of 90 line-pairs/mm (i.e., for M = 0.7071). At a frequency of
r
1000 cycles/mm the modulation M = 0.1, which
r
indicates that features of ~1 mm are resolvable.
X-Ray Generation. We are principally con-
cerned with the deposition of electron beam
energy in thick, or electron-opaque, targets. For
this type of target the energy is mainly converted
internally with the remainder backscattered
externally. The x-ray emission is created by
deceleration of the incident electrons through the
Coulomb interaction with the nuclei of the target
and by the removal of bound atomic electrons
with the subsequent repopulation of the vacant
orbits from adjacent-electron orbits. The former
process relates to a broadband continuous spec-
trum and the latter to a process that produces
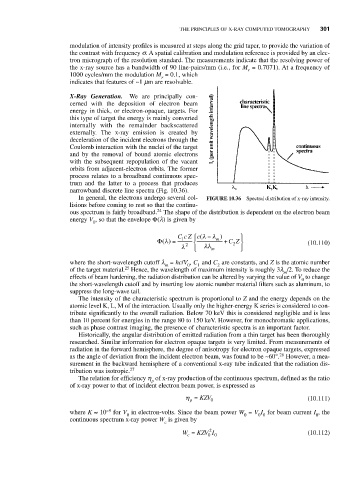
narrowband discrete line spectra (Fig. 10.36).
In general, the electrons undergo several col- FIGURE 10.36 Spectral distribution of x-ray intensity.
lisions before coming to rest so that the continu-
24
ous spectrum is fairly broadband. The shape of the distribution is dependent on the electron beam
energy V , so that the envelope Φ(l) is given by
0
−
Cc Z ⎧ ⎪ c (λλ ) ⎫ ⎪
λ
Φ() = 1 ⎨ m + CZ ⎬ (10.110)
2
λ 2 ⎩ ⎪ λλ m ⎭ ⎪
where the short-wavelength cutoff l = hc/V , C and C are constants, and Z is the atomic number
m
1
2
0
25
of the target material. Hence, the wavelength of maximum intensity is roughly 3l /2. To reduce the
m
effects of beam hardening, the radiation distribution can be altered by varying the value of V to change
0
the short-wavelength cutoff and by inserting low atomic number material filters such as aluminum, to
suppress the long-wave tail.
The intensity of the characteristic spectrum is proportional to Z and the energy depends on the
atomic level K, L, M of the interaction. Usually only the higher-energy K series is considered to con-
tribute significantly to the overall radiation. Below 70 keV this is considered negligible and is less
than 10 percent for energies in the range 80 to 150 keV. However, for monochromatic applications,
such as phase contrast imaging, the presence of characteristic spectra is an important factor.
Historically, the angular distribution of emitted radiation from a thin target has been thoroughly
researched. Similar information for electron opaque targets is very limited. From measurements of
radiation in the forward hemisphere, the degree of anisotropy for electron opaque targets, expressed
26
as the angle of deviation from the incident electron beam, was found to be ~60°. However, a mea-
surement in the backward hemisphere of a conventional x-ray tube indicated that the radiation dis-
tribution was isotropic. 27
The relation for efficiency h of x-ray production of the continuous spectrum, defined as the ratio
p
of x-ray power to that of incident electron beam power, is expressed as
η = KZV 0 (10.111)
p
where K ≈ 10 −9 for V in electron-volts. Since the beam power W = V I for beam current I , the
0 0 0 0 0
continuous spectrum x-ray power W is given by
c
2
W = KZV I (10.112)
c
0 0