Page 203 - Calculus Demystified

CHAPTER 6
190
y Transcendental Functions

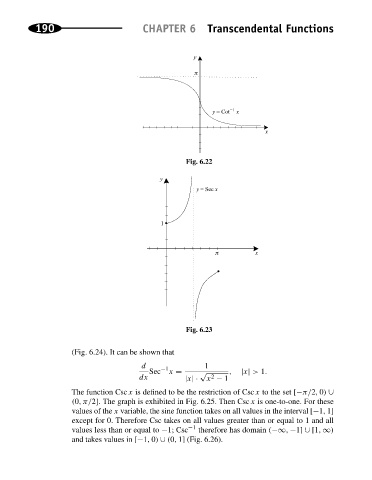
_ 1
y = Cot x

x

Fig. 6.22

y
y = Sec x

1

x

Fig. 6.23

(Fig. 6.24). It can be shown that
d −1 1
Sec x = √ , |x| > 1.
2
dx |x|· x − 1
The function Csc x is defined to be the restriction of Csc x to the set [−π/2, 0) ∪
(0,π/2]. The graph is exhibited in Fig. 6.25. Then Csc x is one-to-one. For these
values of the x variable, the sine function takes on all values in the interval [−1, 1]
except for 0. Therefore Csc takes on all values greater than or equal to 1 and all
values less than or equal to −1; Csc −1 therefore has domain (−∞, −1]∪[1, ∞)
and takes values in [−1, 0) ∪ (0, 1] (Fig. 6.26).