Page 380 - Cam Design Handbook

THB12 9/19/03 7:34 PM Page 368

368 CAM DESIGN HANDBOOK

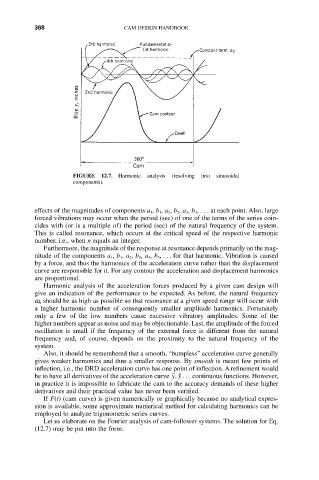
FIGURE 12.7. Harmonic analysis (resolving into sinusoidal
components).

effects of the magnitudes of components a 1, b 1, a 2, b 2, a 3, b 3,...at each point. Also, large
forced vibrations may occur when the period (sec) of one of the terms of the series coin-
cides with (or is a multiple of) the period (sec) of the natural frequency of the system.
This is called resonance, which occurs at the critical speed of the respective harmonic
number, i.e., when n equals an integer.
Furthermore, the magnitude of the response at resonance depends primarily on the mag-
nitude of the components a 1 , b 1 , a 2 , b 2 , a 3 , b 3 ,... for that harmonic. Vibration is caused
by a force, and thus the harmonics of the acceleration curve rather than the displacement
curve are responsible for it. For any contour the acceleration and displacement harmonics
are proportional.
Harmonic analysis of the acceleration forces produced by a given cam design will
give an indication of the performance to be expected. As before, the natural frequency
w n should be as high as possible so that resonance at a given speed range will occur with
a higher harmonic number of consequently smaller amplitude harmonics. Fortunately
only a few of the low numbers cause excessive vibratory amplitudes. Some of the
higher numbers appear as noise and may be objectionable. Last, the amplitude of the forced
oscillation is small if the frequency of the external force is different from the natural
frequency and, of course, depends on the proximity to the natural frequency of the
system.
Also, it should be remembered that a smooth, “bumpless” acceleration curve generally
gives weaker harmonics and thus a smaller response. By smooth is meant few points of
inflection, i.e., the DRD acceleration curve has one point of inflection. A refinement would
be to have all derivatives of the acceleration curve , y ¨ . . . continuous functions. However,
¨
˙˙˙ y
in practice it is impossible to fabricate the cam to the accuracy demands of these higher
derivatives and their practical value has never been verified.
If F(t) (cam curve) is given numerically or graphically because no analytical expres-
sion is available, some approximate numerical method for calculating harmonics can be
employed to analyze trigonometric series curves.
Let us elaborate on the Fourier analysis of cam-follower systems. The solution for Eq.
(12.7) may be put into the form: