Page 378 - Cam Design Handbook

THB12 9/19/03 7:34 PM Page 366

366 CAM DESIGN HANDBOOK

be less than one-thousandth of the amplitude of the first harmonic and thus are unlikely
to cause major problems. These observations also imply that accurate control of the high-
order derivatives is not critical in controlling system vibration.
With the open-track cam-follower system we may have a condition called jump or
bounce. It is a transient condition that occurs with high-speed and highly flexible systems.
With jump, the cam and the follower separate owing to excessively unbalanced forces
exceeding the spring force during the period of negative acceleration. This is undesirable
since the fundamental function of the cam-follower system, the constraint and control of
follower motion, is not maintained. Also related are short life of the cam flank surface,
high noise, vibrations, and poor action.
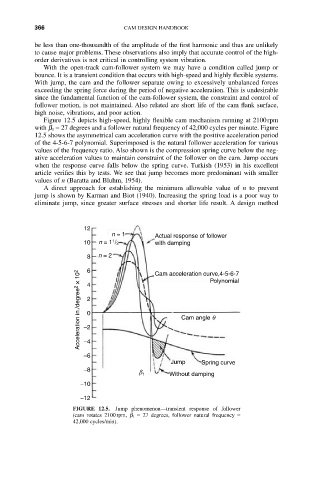
Figure 12.5 depicts high-speed, highly flexible cam mechanism running at 2100rpm
with b 1 = 27 degrees and a follower natural frequency of 42,000 cycles per minute. Figure
12.5 shows the asymmetrical cam acceleration curve with the positive acceleration period
of the 4-5-6-7 polynomial. Superimposed is the natural follower acceleration for various
values of the frequency ratio. Also shown is the compression spring curve below the neg-
ative acceleration values to maintain constraint of the follower on the cam. Jump occurs
when the response curve falls below the spring curve. Turkish (1953) in his excellent
article verifies this by tests. We see that jump becomes more predominant with smaller
values of n (Baratta and Bluhm, 1954).
A direct approach for establishing the minimum allowable value of n to prevent
jump is shown by Karman and Biot (1940). Increasing the spring load is a poor way to
eliminate jump, since greater surface stresses and shorter life result. A design method

12
n = 1 Actual response of follower
1
10 n = 1 / 2 with damping
8 n = 2 Cam acceleration curve,4-5-6-7
6
Acceleration in./degree 2 ¥ 10 2 -2 Cam angle q
Polynomial
4
2
0

-4

-6
Jump Spring curve
-8 b 1 Without damping
-10

-12
FIGURE 12.5. Jump phenomenon—transient response of follower
(cam rotates 2100rpm, b 1 = 27 degrees, follower natural frequency =
42,000 cycles/min).