Page 383 - Cam Design Handbook

THB12 9/19/03 7:34 PM Page 371

CAM SYSTEM DYNAMICS—ANALYSIS 371

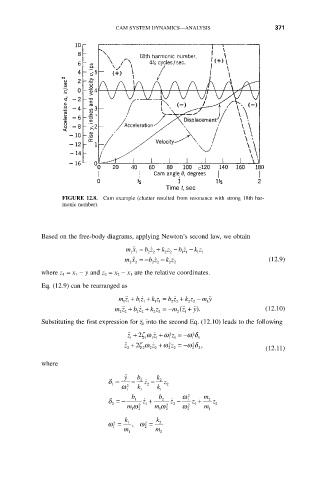
FIGURE 12.8. Cam example (chatter resulted from resonance with strong 18th har-
monic number).

Based on the free-body diagrams, applying Newton’s second law, we obtain
mx ˙˙ = b z ˙ + k z - b z ˙ - k z
1 1
22
1 1
22
1 1
mx ˙˙ =- b z ˙ - k z (12.9)
2 2 22 22
where z 1 = x 1 - y and z 2 = x 2 - x 1 are the relative coordinates.
Eq. (12.9) can be rearranged as
mz ˙˙ + b z ˙ + k z = b z ˙ + k z - m y ˙˙
11 11 11 2 2 2 2 1
(
y ˙˙ .
mz ˙˙ + b z ˙ + k z = - m z ˙˙ + ) (12.10)
22 22 22 2 1
Substituting the first expression for z 1 into the second Eq. (12.10) leads to the following
¨
˙˙ z + 2zw ˙ z +w 2 z = -w d
2
1 1 1 1 1 1 1 1
2
˙˙ z + 2zw ˙ z +w 2 z = -w d ,
2 2 2 2 2 2 2 2 (12.11)
where
˙˙ y b k
d = - 2 ˙ z - 2 z
1 2 2
w 2 k k
1 1 1
b b w 2 m
d =- 1 ˙ z + 2 ˙ z - 1 z + 2 z
2 1 2 1 2
m w 2 m w 2 w 2 m
1 2 1 2 2 1
k k
w = 1 , w = 2
2
2
1 2
m m
1 2