Page 455 - Cam Design Handbook

THB13 9/19/03 7:56 PM Page 443

CAM SYSTEM DYNAMICS—RESPONSE 443

5-6-7-8-9 Follower end
+0.016
acceleration y ≤

4-5-6-7 Follower end
+0.008
Acceleration, in./deg. 2 –0.008 acceleration y ≤ c
acceleration y ≤
0
5-6-7-8-9 cam
acceleration y ≤
4-5-6-7 cam
c

–0.016

0 15 30 45 60
Cam angle q
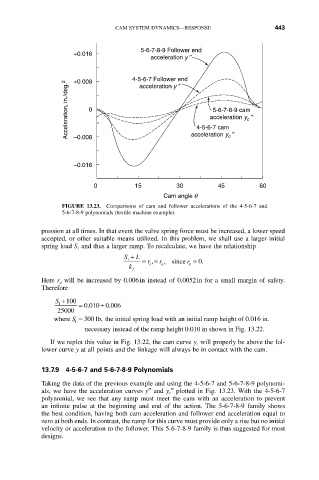
FIGURE 13.23. Comparisons of cam and follower accelerations of the 4-5-6-7 and
5-6-7-8-9 polynomials (textile machine example).
pression at all times. In that event the valve spring force must be increased, a lower speed
accepted, or other suitable means utilized. In this problem, we shall use a larger initial
spring load S 1 and thus a larger ramp. To recalculate, we have the relationship
S + L = r =, r , since r = 0.
1
k f s a k
Here r a will be increased by 0.006in instead of 0.0052in for a small margin of safety.
Therefore
S + 100
1 = . + .
0 010 0 006
25000
where S = 300 lb, the initial spring load with an initial ramp height of 0.016 in.
1
necessary instead of the ramp height 0.010 in shown in Fig. 13.22.
If we replot this value in Fig. 13.22, the cam curve y c will properly be above the fol-
lower curve y at all points and the linkage will always be in contact with the cam.

13.7.9 4-5-6-7 and 5-6-7-8-9 Polynomials
Taking the data of the previous example and using the 4-5-6-7 and 5-6-7-8-9 polynomi-
als, we have the acceleration curves y≤ and y c≤ plotted in Fig. 13.23. With the 4-5-6-7
polynomial, we see that any ramp must meet the cam with an acceleration to prevent
an infinite pulse at the beginning and end of the action. The 5-6-7-8-9 family shows
the best condition, having both cam acceleration and follower end acceleration equal to
zero at both ends. In contrast, the ramp for this curve must provide only a rise but no initial
velocity or acceleration to the follower. This 5-6-7-8-9 family is thus suggested for most
designs.