Page 184 - Carbon Nanotubes

et
176 U. ZIMMERMAN al.
'""' 12
1 LiXC60". ' "'

I
12 j
4 4 x=7 n
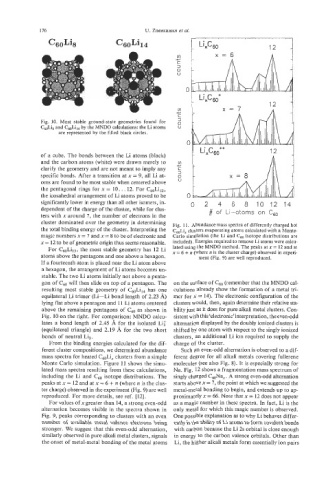
Fig. 10. Most stable ground-state geometries found for
Cdi, and C&i14 by the MNDO calculations: the Li atoms
are represented by the filled black circles.

I Li,C6," ? J
of a cube. The bonds between the Li atoms (black)
and the carbon atoms (white) were drawn merely to
clarify the geometry and are not meant to imply any
specific bonds. After a transition at x = 9, all Li at-
oms are found to be most stable when centered above
the pentagonal rings for x = 10. . . 12. For C6,,Li12,
the icosahedral arrangement of Li atoms proved to be
significantly lower in energy than all other isomers, in- 0 2 4 6 8101214
dependent of the charge of the cluster, while for clus- # of Li-atoms on c,,
ters with x around 7, the number of electrons in the
cluster dominated over the geometry in determining Fig. 11. Abundance mass spectra of differently charged hot
the total binding energy of the cluster. Interpreting the C,,Li, clusters evaporating atoms calculated with a Monte-
magic numbers x = 7 and x = 8 to be of electronic and Carlo simulation (the Li and C,, isotope distributions are
x = 12 to be of geometric origin thus seems reasonable. included). Energies required to remove Li atoms were calcu-
For CsoLi13, the most stable geometry has 12 Li lated using the MNDO method. The peaks at x = 12 and at
x = 6 + n (where n is the cluster charge) observed in experi-
atoms above the pentagons and one above a hexagon. ment (Fig. 9) are well reproduced.
If a fourteenth atom is placed near the Li atom above
a hexagon, the arrangement of Li atoms becomes un-
stable. The two Li atoms initially not above a penta-
gon of c6(, will then slide on top of a pentagon. The on the surface of Cs0 (remember that the MNDO cal-
resulting most stable geometry of C60Li,4 has one culations already show the formation of a metal tri-
equilateral Li trimer (Li-Li bond length of 2.23 A) mer for x = 14). The electronic configuration of the
lying flat above a pentagon and 11 Li atoms centered clusters would, then, again determine their relative sta-
above the remaining pentagons of C,o as shown in bility just as it does for pure alkali metal clusters. Con-
Fig. 10 on the right. For comparison: MNDO calcu- sistent with this 'electronic'interpretation, the even-odd
lates a bond length of 2.45 A for the isolated Li: alternation displayed by the doubly ionized clusters is
(equilateral triangle) and 2.19 A for the two short shifted by one atom with respect to the singly ionized
bonds of neutral Li3. clusters, an additional Li ion required to supply the
From the binding energies calculated for the dif- charge of the cluster.
ferent cluster compositions, we determined abundance Such an even-odd alternation is observed to a dif-
mass spectra for heated C6,LiX clusters from a simple ferent degree for all alkali metals covering fullerene
Monte Carlo simulation. Figure 11 shows the simu- molecules (see also Fig. 8). It is especially strong for
lated mass spectra resulting from these calculations, Na. Fig. 12 shows a fragmentation mass spectrum of
including the Li and C, isotope distributions. The singly charged C&ax. A strong even-odd alternation
peaks at x = 12 and at x = 6 + n (where n is the clus- starts above x = 7, the point at which we suggested the
ter charge) observed in the experiment (Fig. 9) are well metal-metal bonding to begin, and extends up to ap-
reproduced. For more details, see ref. [12]. proximately x = 66. Note that x = 12 does not appear
For values of x greater than 14, a strong even-odd as a magic number in these spectra. In fact, Li is the
alternation becomes visible in the spectra shown in only metal for which this magic number is observed.
Fig. 9, peaks corresponding to clusters with an even One possible explanation as to why Li behaves differ-
number of available metal valence electrons being ently is the ability of Li atoms to form covalent bonds
stronger. We suggest that this even-odd alternation, with carbon because the Li 2s orbital is close enough
similarly observed in pure alkali metal clusters, signals in energy to the carbon valence orbitals. Other than
the onset of metal-metal bonding of the metal atoms Li, the higher alkali metals form essentially ion pairs