Page 129 - Chalcogenide Glasses for Infrared Optics

106 Cha pte r F o u r

repeated until the approximate maximum intensity angle is located.
The computer-controlled process locates the approximate angle pro-
ducing the greatest signal. A scan is then made in exact angle incre-
ments three stops on each side of the peak intensity with one near the
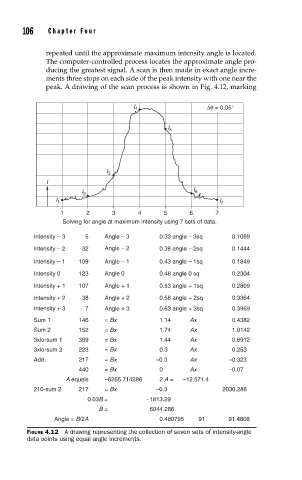
peak. A drawing of the scan process is shown in Fig. 4.12, marking

∆θ = 0.05°
I 4

I 5

I 3
I
I 6
I 2
I 1 I 7
1 2 3 4 5 6 7
Solving for angle at maximum intensity using 7 sets of data.

Intensity – 3 5 Angle – 3 0.33 angle – 3sq 0.1089
Intensity – 2 32 Angle – 2 0.38 angle – 2sq 0.1444
Intensity – 1 109 Angle – 1 0.43 angle – 1sq 0.1849
Intensity 0 123 Angle 0 0.48 angle 0 sq 0.2304
Intensity + 1 107 Angle + 1 0.53 angle + 1sq 0.2809
Intensity + 2 38 Angle + 2 0.58 angle + 2sq 0.3364
Intensity + 3 7 Angle + 3 0.63 angle + 3sq 0.3969
Sum 1 146 = Bx 1.14 Ax 0.4382
Sum 2 152 = Bx 1.74 Ax 1.0142
3xlo-sum 1 369 = Bx 1.44 Ax 0.6912
3xlo-sum 2 223 = Bx 0.3 Ax 0.253
Add 217 = Bx –0.3 Ax –0.323
440 = Bx 0 Ax –0.07
A equals –6265.714286 2 A = –12,571.4
210-sum 2 217 = Bx –0.3 2030.286
0.03B = –1813.29
B = 6044.286
Angle = B/2A 0.480795 91 91.4808
FIGURE 4.12 A drawing representing the collection of seven sets of intensity-angle
data points using equal angle increments.