Page 135 - Chemical Process Equipment - Selection and Design

6.6. NON-NEWTONIAN LIQUIDS 107

EXAMPLE 63 equation
Analysis of Data Qhtahed in a Capillary Tube Viscometer
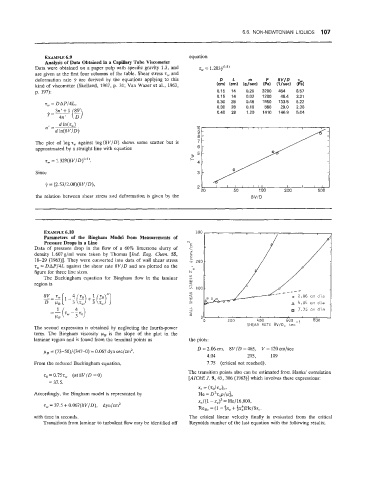
Data were obtained on a paper pulp withi specific gravity 1.3, and z, = 1.203j0.51
are given as the first four columns of the table. Shear stress z,,, and
deformation rate i. are derived by the equations applying to this D L rh P av/v
kind of viscometer (Skelland, 1967, p. 31; Van Wazer et al., 1963, Icm) (cm) Wsed (Pa) (l/sed (Pa)
p. 197): 0.15 14 0.20 3200 464 8.57
0.15 14 0.02 1200 46.4 3.21
z, = D AP/4L, 0.30 28 0.46 1950 133.5 5.22
0.30 28 0.10 860 29.0 2.30
0.40 28 1.20 1410 146.9 5.04

d Mzw)
n' =d ln(8VID)
The plot of lopz, against log(8VID) shows some scatter but is
approximated by a straight line with equation
7;, = 1.329(8V/D)0.5f,

Since
9 = (2.53/:!.08)(8V/D),
2' I I I I I I I I I I I 1
20 50 100 200 500
the relation between shear stress and deformation is given by the 8VlD

EXAMPLE 6-10 300, r
Parametem of the Bingham Modell from Measurements of
Pressure Dlrops in a Line
Data of pressure drop in the flow of a 60% limestone slurry of
density 1.607gfml were taken by Thomas [Ind. Eng. Chem. 55,
18-29 (1963)l. They were converted into data of wall shear stress
z, = DAP/4L against the shear rate 8VID and are plotted on the
figure for three line sizes.
The Buckingham equation for Bingham flow in the laminar
region is

2.06 cm dia
A 4.04 cm dia 4
7.75 cm dia
0
0 200 400 600 800
The second expression is obtained by neglecting the fourth-power SHEAR RATE 8V/D, sec
term. The Bingham viscosity pB is the slope of the plot in the
laminar region and is falund from the terminal points as the plots:
pB = (73-.50)/(347-0) = 0.067 dyn sec/cm*. D = 2.06 cm, 8V/D = 465, V = 120 cmfsec
4.04 215, 109
From the reduced Buckingham equation, 7.75 (critical not reached).
The transition points also can be estimated from Hanks' correlation
zo = 0.75~,, (at 8V/D = 0) [AZChE J. 9,45, 306 (1963)l which involves these expressions:
= 37.5.
xc = (%/z,),>
Accordingly, the Bingham model is represented by He = D2z@/&.,
xJ(1- xJ3 = He/16,800,
zw = 37.5 I- 0.067@V/D), dyn/cd
ReB, = (1 - $xc + $x$)He/8xC.
with time in seconds. The critical linear velocity finally is evaluated from the critical
Transitions from laminar to turbulent flow may be identified off Reynolds number of the last equation with the following results;