Page 160 - Chemical Process Equipment - Selection and Design

132 FLUID TRANSPORT EQUIPMENT

EXAMPLE 7.1 P= pn3D5C, = 1000(400/60)3(2)5(0.69)
Application of Dimensionless Performance Curves = 6.54(106) kgm2/sec3,
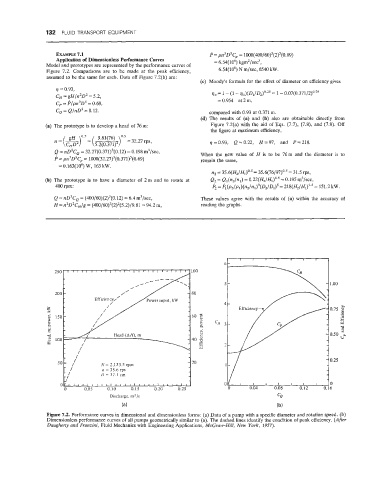
Model and prototypes are represented by the performance curves of
Figure 7.2. Comparisons are to be made at the peak efficiency, 6.54(106) N m/sec, 6540 kW.
assumed to be the same for each. Data off Figure 7.2(b) are:
(c) Moody’s formula for the effect of diameter on efficiency gives
q = 0.93,
1
=
C, = gH/n2D2 = 5.2, v2 = 1 - (1 - 71)(D1/Dz)0.’5 - 0.07(0.371/2)0.25
C, = P/pn3D5 = 0.69, =0.954 at2m,
C, = Q/nD3 = 0.12. compared with 0.93 at 0.371 m.
(a) The results of (a) and (b) also are obtainable directly from
(a) The prototype is to develop a head of 76 m: Figure 7.2(a) with the aid of Eqs. (7.7), (7.8), and (7.9). Off
the figure at maximum efficiency,
r] =0.93, Q=O.22, H=97, and P=218.
Q = nD3CQ = 32.27(0.371)3(0. 12) = 0.198 m3/sec, When the new value of H is to be 76m and the diameter is to
P = pn3D5Cp = 1000(32.27)3(0.371)5(0.69) remain the same,
= 0.163(106) W, 163 kW.
n, = 35.6(H2/H1)0’5 = 35.6(76/97)0.5 = 31.5 rps,
(b) The prototype is to have a diameter of 2m and to rotate at Qz = Ql(n2/nl) = 0.22(H2/H1)0.5 = 0.195 m3/sec,
400 rpm: kz = ~,(p,/p,)(n2/nl)3(D2/D,)5 218(H2/H1)1.5 = 151.2 kW.
=
Q = nD3CQ = (400/60)(2)3(0.12) = 6.4 m3/sec, These values agree with the results of (a) within the accuracy of
H = n2D2C,/g = (400/60)2(2)2(5.2)/9.81 = 94.2 m, reading the graphs.

Discharge. m3 /s CQ
(a) (b)
Figure 7.2. Performance curves in dimensional and dimensionless forms: (a) Data of a pump with a specific diameter and rotation speed. (b)
Dimensionless performance curves of all pumps geometrically similar to (a). The dashed lines identify the condition of peak efficiency. (After
Daugherty and Franzini, Fluid Mechanics with Engineering Applications, McGraw-Hill, New York, 1957).