Page 146 - Chemical equilibria Volume 4

122 Chemical Equilibria
The distance (in terms of frequency) between two spectral lines in the
same series, obtained for two consecutive values v and v + 1, will therefore
be:
⎡ hν ⎤
−
+
v1
Δ ν abs = ν vibr ⎢ 12 vibr (v1 ) ⎥ [4.29]
+
v
⎣ 4E ∞ ⎦
This distance shrinks as v increases, until it finally disappears entirely.
Thus, the vibrational energy cannot surpass a certain limit. If we give the
molecule more energy than that limit, it dissociates. This results in the
presence of a continuous adsorption spectrum beyond a certain value v lim of
+
v, so that the difference Δ v1 E = 0 , which gives us the value:
v
1 2E
v lim = − 1= ∞ − 1 [4.30]
2x hν vibr

The energy of dissociation is therefore equal to the difference between
the minimal energy (obtained for v = 0) and this limit energy denoted
.
by E Thus, we write:
∞
D = E − E v0 [4.31]
∞
=
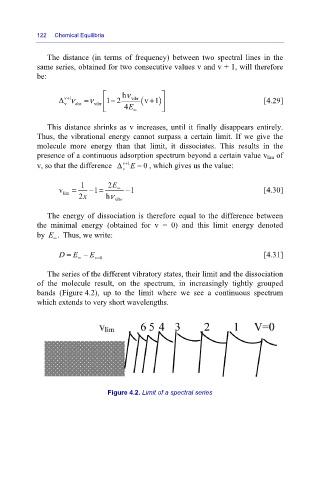
The series of the different vibratory states, their limit and the dissociation
of the molecule result, on the spectrum, in increasingly tightly grouped
bands (Figure 4.2), up to the limit where we see a continuous spectrum
which extends to very short wavelengths.

Figure 4.2. Limit of a spectral series