Page 354 - Computational Fluid Dynamics for Engineers

344 11. Incompressible Navier-Stokes Equations

0.01 Or-
0007
0009 *'
• 1/7th power-law Rx = 0.80 10 7 . 0.006 _ • Empirical law
0 008 INS2DRx = 0.80 10 7 Y _, • INS2D
0.007 • •• 0 005
0006 • - •
• : 0004 - •, " I I
y 0005 X
• c, <S^^
r 0 003 " ^ ^ ^ ^ j ! ^ ^ ^ ^
0.004
4 „
0.003 0.002 ~
0.002 _/
J 0001
0001
^ . • . o ' . . . 1 . . . . I • • • • 1 . . . . 1 . • , I • • • • l • • • . 1
0.000' 0 1E+06 2E+06 3E+06 . 4E+06 5E+06 6E+06 7E+06
5 0.5 1
(a) u/U e (b) X
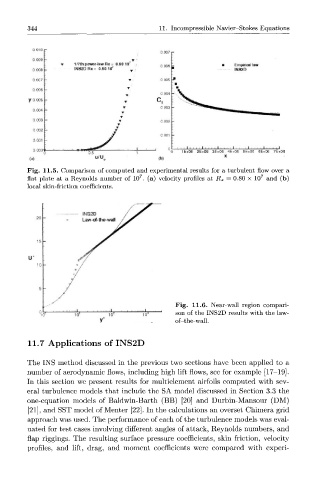
Fig. 11.5. Comparison of computed and experimental results for a turbulent flow over a
7
flat plate at a Reynolds number of 10 . (a) velocity profiles at R x =0.80 x 10 7 and (b)
local skin-friction coefficients.

INS2D
Law-of-the-wall

Fig. 11.6. Near-wall region compari-
son of the INS2D results with the law-
10'
of-the-wall.

11.7 Applications of INS2D

The INS method discussed in the previous two sections have been applied to a
number of aerodynamic flows, including high lift flows, see for example [17-19].
In this section we present results for multielement airfoils computed with sev-
eral turbulence models that include the SA model discussed in Section 3.3 the
one-equation models of Baldwin-Barth (BB) [20] and Durbin-Mansour (DM)
[21], and SST model of Menter [22]. In the calculations an overset Chimera grid
approach was used. The performance of each of the turbulence models was eval-
uated for test cases involving different angles of attack, Reynolds numbers, and
flap riggings. The resulting surface pressure coefficients, skin friction, velocity
profiles, and lift, drag, and moment coefficients were compared with experi-