Page 357 - Computational Fluid Dynamics for Engineers

11.7 Applications of INS2D 347

-0.100 -(II)"? -0 0*0 -M025 "000 !M I 02 i)-; it4 o? of) 0 " OH ovo 0'>s i oo I o? | io I I ?
(a)

Slat
BB
"*V t " "" SA
SST
DM
J/-
•V • -— r " ""

-0 100 -fid"? -0 0?!l -D02? 0-000 I 00 l.o? I 10 II ?
(b)
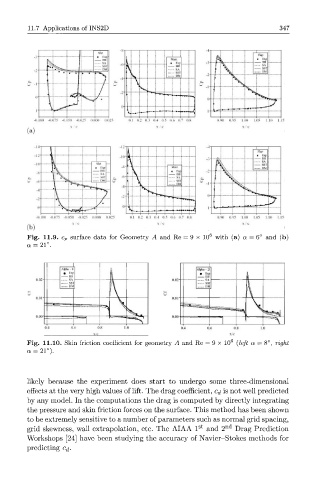
Fig. 11.9. c p surface data for Geometry A and Re = 9 x 10 6 with (a) a = 6° and (b)
a = 21°.

Alpha 8 Alpha 2
i
HB m i-xp
\)U
0.02- SA SA
- ss - ss
DM
DM A
w—• > •»-
H \ ^Sk*. »*Mt
I , ^ j

Fig. 11.10. Skin friction coefficient for geometry A and Re = 9 x 10 (left a = 8°, right
a = 21°).

likely because the experiment does start to undergo some three-dimensional
effects at the very high values of lift. The drag coefficient, c^ is not well predicted
by any model. In the computations the drag is computed by directly integrating
the pressure and skin friction forces on the surface. This method has been shown
to be extremely sensitive to a number of parameters such as normal grid spacing,
st n d
grid skewness, wall extrapolation, etc. The AIAA 1 and 2 Drag Prediction
Workshops [24] have been studying the accuracy of Navier-Stokes methods for
predicting Q .