Page 145 - Computational Modeling in Biomedical Engineering and Medical Physics

134 Computational Modeling in Biomedical Engineering and Medical Physics

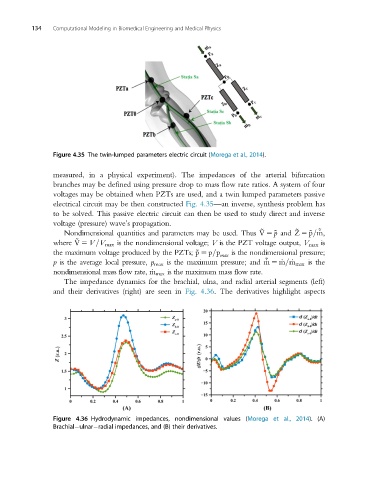
Figure 4.35 The twin-lumped parameters electric circuit (Morega et al., 2014).

measured, in a physical experiment). The impedances of the arterial bifurcation
branches may be defined using pressure drop to mass flow rate ratios. A system of four
voltages may be obtained when PZTs are used, and a twin lumped parameters passive
electrical circuit may be then constructed Fig. 4.35—an inverse, synthesis problem has
to be solved. This passive electric circuit can then be used to study direct and inverse
voltage (pressure) wave’s propagation.
~
Nondimensional quantities and parameters may be used. Thus ~ V 5 ~p and ~ Z 5 ~p= _m,
where ~ V 5 V=V max is the nondimensional voltage; V is the PZT voltage output, V max is
themaximum voltageproduced bythe PZTs; ~p 5 p=p is the nondimensional pressure;
max
~
p is the average local pressure, p max is the maximum pressure; and _m 5 _m= _m max is the
nondimensional mass flow rate, _m max is the maximum mass flow rate.
The impedance dynamics for the brachial, ulna, and radial arterial segments (left)
and their derivatives (right) are seen in Fig. 4.36. The derivatives highlight aspects

Figure 4.36 Hydrodynamic impedances, nondimensional values (Morega et al., 2014). (A)
Brachial ulnar radial impedances, and (B) their derivatives.