Page 279 -

258 5 Segmentation

f '(x k)
m(x k) f (x)
K(x)

x i G(x) x k x

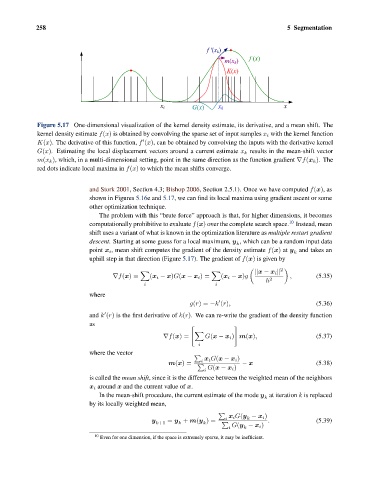
Figure 5.17 One-dimensional visualization of the kernel density estimate, its derivative, and a mean shift. The
kernel density estimate f(x) is obtained by convolving the sparse set of input samples x i with the kernel function

K(x). The derivative of this function, f (x), can be obtained by convolving the inputs with the derivative kernel
G(x). Estimating the local displacement vectors around a current estimate x k results in the mean-shift vector
m(x k ), which, in a multi-dimensional setting, point in the same direction as the function gradient ∇f(x k ). The
red dots indicate local maxima in f(x) to which the mean shifts converge.

and Stork 2001, Section 4.3; Bishop 2006, Section 2.5.1). Once we have computed f(x),as
shown in Figures 5.16e and 5.17, we can find its local maxima using gradient ascent or some
other optimization technique.
The problem with this “brute force” approach is that, for higher dimensions, it becomes
computationally prohibitive to evaluate f(x) over the complete search space. 10 Instead, mean
shift uses a variant of what is known in the optimization literature as multiple restart gradient
descent. Starting at some guess for a local maximum, y , which can be a random input data
k
point x i , mean shift computes the gradient of the density estimate f(x) at y and takes an
k
uphill step in that direction (Figure 5.17). The gradient of f(x) is given by
2

x − x i

∇f(x)= (x i − x)G(x − x i )= (x i − x)g , (5.35)
h 2
i i
where

g(r)= −k (r), (5.36)
and k (r) is the first derivative of k(r). We can re-write the gradient of the density function

as

∇f(x)= G(x − x i ) m(x), (5.37)
i
where the vector

x i G(x − x i )
i
m(x)= − x (5.38)
G(x − x i )
i
is called the mean shift, since it is the difference between the weighted mean of the neighbors
x i around x and the current value of x.
In the mean-shift procedure, the current estimate of the mode y at iteration k is replaced
k
by its locally weighted mean,
x i G(y − x i )

k
i
y . (5.39)
k
k+1 = y + m(y )=
k
k
i G(y − x i )
10 Even for one dimension, if the space is extremely sparse, it may be inefficient.