Page 283 -

262 5 Segmentation

(a) (b)

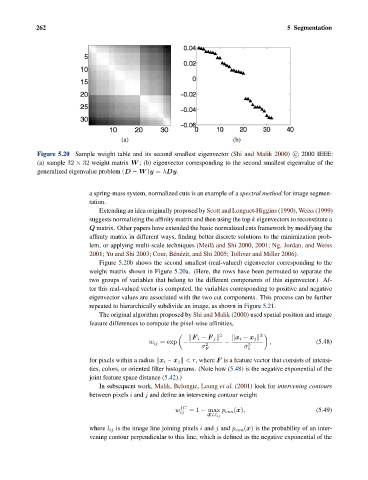
Figure 5.20 Sample weight table and its second smallest eigenvector (Shi and Malik 2000) c 2000 IEEE:
(a) sample 32 × 32 weight matrix W ; (b) eigenvector corresponding to the second smallest eigenvalue of the
generalized eigenvalue problem (D − W )y = λDy.

a spring-mass system, normalized cuts is an example of a spectral method for image segmen-
tation.
Extending an idea originally proposed by Scott and Longuet-Higgins (1990), Weiss (1999)
suggests normalizing the affinity matrix and then using the top k eigenvectors to reconstitute a
Q matrix. Other papers have extended the basic normalized cuts framework by modifying the
affinity matrix in different ways, finding better discrete solutions to the minimization prob-
lem, or applying multi-scale techniques (Meil˘ a and Shi 2000, 2001; Ng, Jordan, and Weiss
2001; Yu and Shi 2003; Cour, B´ en´ ezit, and Shi 2005; Tolliver and Miller 2006).
Figure 5.20b shows the second smallest (real-valued) eigenvector corresponding to the
weight matrix shown in Figure 5.20a. (Here, the rows have been permuted to separate the
two groups of variables that belong to the different components of this eigenvector.) Af-
ter this real-valued vector is computed, the variables corresponding to positive and negative
eigenvector values are associated with the two cut components. This process can be further
repeated to hierarchically subdivide an image, as shown in Figure 5.21.
The original algorithm proposed by Shi and Malik (2000) used spatial position and image
feature differences to compute the pixel-wise affinities,

2 2

F i − F j x i − x j
w ij = exp − 2 − , (5.48)
σ σ 2
F s
for pixels within a radius x i − x j <r, where F is a feature vector that consists of intensi-
ties, colors, or oriented filter histograms. (Note how (5.48) is the negative exponential of the
joint feature space distance (5.42).)
In subsequent work, Malik, Belongie, Leung et al. (2001) look for intervening contours
between pixels i and j and define an intervening contour weight

w IC =1 − max p con (x), (5.49)
ij
x∈l ij
where l ij is the image line joining pixels i and j and p con (x) is the probability of an inter-
vening contour perpendicular to this line, which is defined as the negative exponential of the