Page 288 -

5.5 Graph cuts and energy-based methods 267

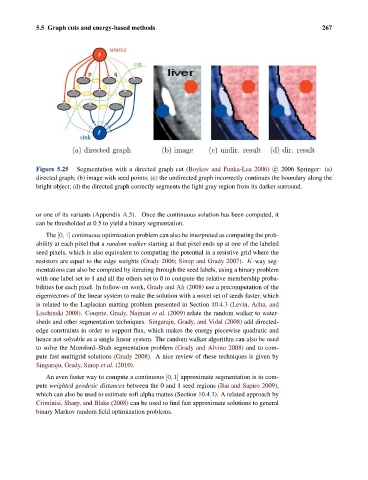
Figure 5.25 Segmentation with a directed graph cut (Boykov and Funka-Lea 2006) c 2006 Springer: (a)
directed graph; (b) image with seed points; (c) the undirected graph incorrectly continues the boundary along the
bright object; (d) the directed graph correctly segments the light gray region from its darker surround.

or one of its variants (Appendix A.5). Once the continuous solution has been computed, it
can be thresholded at 0.5 to yield a binary segmentation.
The [0, 1] continuous optimization problem can also be interpreted as computing the prob-
ability at each pixel that a random walker starting at that pixel ends up at one of the labeled
seed pixels, which is also equivalent to computing the potential in a resistive grid where the
resistors are equal to the edge weights (Grady 2006; Sinop and Grady 2007). K-way seg-
mentations can also be computed by iterating through the seed labels, using a binary problem
with one label set to 1 and all the others set to 0 to compute the relative membership proba-
bilities for each pixel. In follow-on work, Grady and Ali (2008) use a precomputation of the
eigenvectors of the linear system to make the solution with a novel set of seeds faster, which
is related to the Laplacian matting problem presented in Section 10.4.3 (Levin, Acha, and
Lischinski 2008). Couprie, Grady, Najman et al. (2009) relate the random walker to water-
sheds and other segmentation techniques. Singaraju, Grady, and Vidal (2008) add directed-
edge constraints in order to support flux, which makes the energy piecewise quadratic and
hence not solvable as a single linear system. The random walker algorithm can also be used
to solve the Mumford–Shah segmentation problem (Grady and Alvino 2008) and to com-
pute fast multigrid solutions (Grady 2008). A nice review of these techniques is given by
Singaraju, Grady, Sinop et al. (2010).
An even faster way to compute a continuous [0, 1] approximate segmentation is to com-
pute weighted geodesic distances between the 0 and 1 seed regions (Bai and Sapiro 2009),
which can also be used to estimate soft alpha mattes (Section 10.4.3). A related approach by
Criminisi, Sharp, and Blake (2008) can be used to find fast approximate solutions to general
binary Markov random field optimization problems.