Page 362 - Decision Making Applications in Modern Power Systems

324 Decision Making Applications in Modern Power Systems

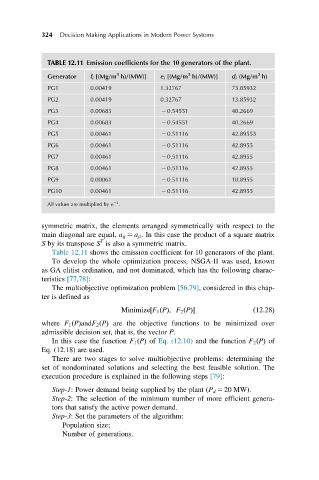
TABLE 12.11 Emission coefficients for the 10 generators of the plant.
3
3
3
Generator f i [(Mg/m h)/(MW)] e i [(Mg/m h)/(MW)] d i (Mg/m h)
PG1 0.00419 1.32767 73.85932
PG2 0.00419 0.32767 13.85932
PG3 0.00683 2 0.54551 40.2669
PG4 0.00683 2 0.54551 40.2669
PG5 0.00461 2 0.51116 42.89553
PG6 0.00461 2 0.51116 42.8955
PG7 0.00461 2 0.51116 42.8955
PG8 0.00461 2 0.51116 42.8955
PG9 0.00061 2 0.51116 10.8955
PG10 0.00461 2 0.51116 42.8955
All values are multiplied by e 22 :

symmetric matrix, the elements arranged symmetrically with respect to the
main diagonal are equal, a ij 5 a ji . In this case the product of a square matrix
T
S by its transpose S is also a symmetric matrix.
Table 12.11 shows the emission coefficient for 10 generators of the plant.
To develop the whole optimization process, NSGA-II was used, known
as GA elitist ordination, and not dominated, which has the following charac-
teristics [77,78]:
The multiobjective optimization problem [56,79], considered in this chap-
ter is defined as
Minimize½F 1 PðÞ; F 2 ðPފ ð12:28Þ
where F 1 PðÞandF 2 ðPÞ are the objective functions to be minimized over
admissible decision set, that is, the vector P:
In this case the function F 1 PðÞ of Eq. (12.10) and the function F 2 PðÞ of
Eq. (12.18) are used.
There are two stages to solve multiobjective problems: determining the
set of nondominated solutions and selecting the best feasible solution. The
execution procedure is explained in the following steps [79]:
Step-1: Power demand being supplied by the plant (P d 5 20 MW).
Step-2: The selection of the minimum number of more efficient genera-
tors that satisfy the active power demand.
Step-3: Set the parameters of the algorithm:
Population size;
Number of generations.