Page 388 - Design of Reinforced Masonry Structures

WALLS UNDER GRAVITY AND TRANSVERSE LOADS 6.39

e u
Floor P uf
P uf e

t
h/2

h w u h 2 ∆u
w u P uf e/2 P ∆u
uf
8
h/2
Base assumed
hinged
(a) (b) (c) (d) (e) (f)

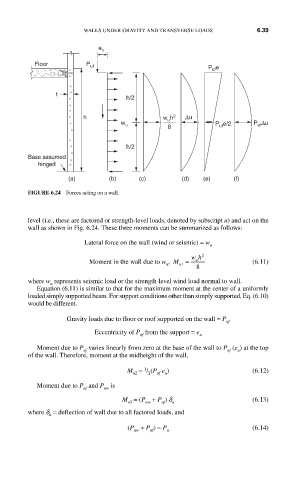
FIGURE 6.24 Forces acting on a wall.

level (i.e., these are factored or strength-level loads, denoted by subscript u) and act on the
wall as shown in Fig. 6.24. These three moments can be summarized as follows:

Lateral force on the wall (wind or seismic) = w
u
u
Moment in the wall due to w , M = wh 2 (6.11)
u
u1
8
where w represents seismic load or the strength-level wind load normal to wall.
u
Equation (6.11) is similar to that for the maximum moment at the center of a uniformly
loaded simply supported beam. For support conditions other than simply supported, Eq. (6.10)
would be different.
Gravity loads due to floor or roof supported on the wall = P uf
Eccentricity of P from the support = e u
uf
Moment due to P uf varies linearly from zero at the base of the wall to P (e ) at the top
u
uf
of the wall. Therefore, moment at the midheight of the wall,
1
M = / (P e ) (6.12)
u2 2 uf u
Moment due to P and P is
uf uw
M = (P + P ) d (6.13)
u
uw
u3
uf
where d = deflection of wall due to all factored loads, and
u
(P + P ) = P (6.14)
uw
uf
u