Page 234 - Distributed model predictive control for plant-wide systems

208 Distributed Model Predictive Control for Plant-Wide Systems

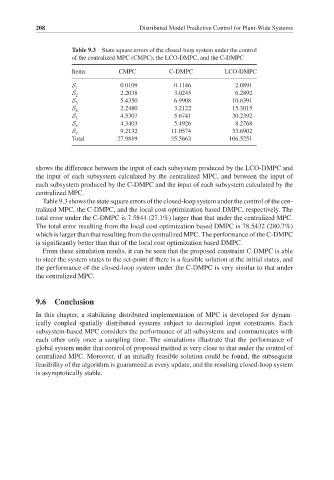
Table 9.3 State square errors of the closed-loop system under the control
of the centralized MPC (CMPC), the LCO-DMPC, and the C-DMPC
Items CMPC C-DMPC LCO-DMPC

S 1 0.0109 0.1146 2.0891
S 2 2.2038 3.0245 6.2892
S 3 5.4350 6.9908 10.6391
S 4 2.2480 3.2122 15.3015
S 5 4.5307 5.6741 30.2392
S 4.3403 5.4926 8.2768
6
S 9.2132 11.0574 33.6902
7
Total 27.9819 35.5663 106.5251

shows the difference between the input of each subsystem produced by the LCO-DMPC and
the input of each subsystem calculated by the centralized MPC, and between the input of
each subsystem produced by the C-DMPC and the input of each subsystem calculated by the
centralized MPC.
Table 9.3 shows the state square errors of the closed-loop system under the control of the cen-
tralized MPC, the C-DMPC, and the local cost optimization based DMPC, respectively. The
total error under the C-DMPC is 7.5844 (27.1%) larger than that under the centralized MPC.
The total error resulting from the local cost optimization based DMPC is 78.5432 (280.7%)
which is larger than that resulting from the centralized MPC. The performance of the C-DMPC
is significantly better than that of the local cost optimization based DMPC.
From these simulation results, it can be seen that the proposed constraint C-DMPC is able
to steer the system states to the set-point if there is a feasible solution at the initial states, and
the performance of the closed-loop system under the C-DMPC is very similar to that under
the centralized MPC.

9.6 Conclusion
In this chapter, a stabilizing distributed implementation of MPC is developed for dynam-
ically coupled spatially distributed systems subject to decoupled input constraints. Each
subsystem-based MPC considers the performance of all subsystems and communicates with
each other only once a sampling time. The simulations illustrate that the performance of
global system under that control of proposed method is very close to that under the control of
centralized MPC. Moreover, if an initially feasible solution could be found, the subsequent
feasibility of the algorithm is guaranteed at every update, and the resulting closed-loop system
is asymptotically stable.